Special Right Triangles
Trig Ratios
Find the Side
Find the Angle
Solving Right Triangles
1
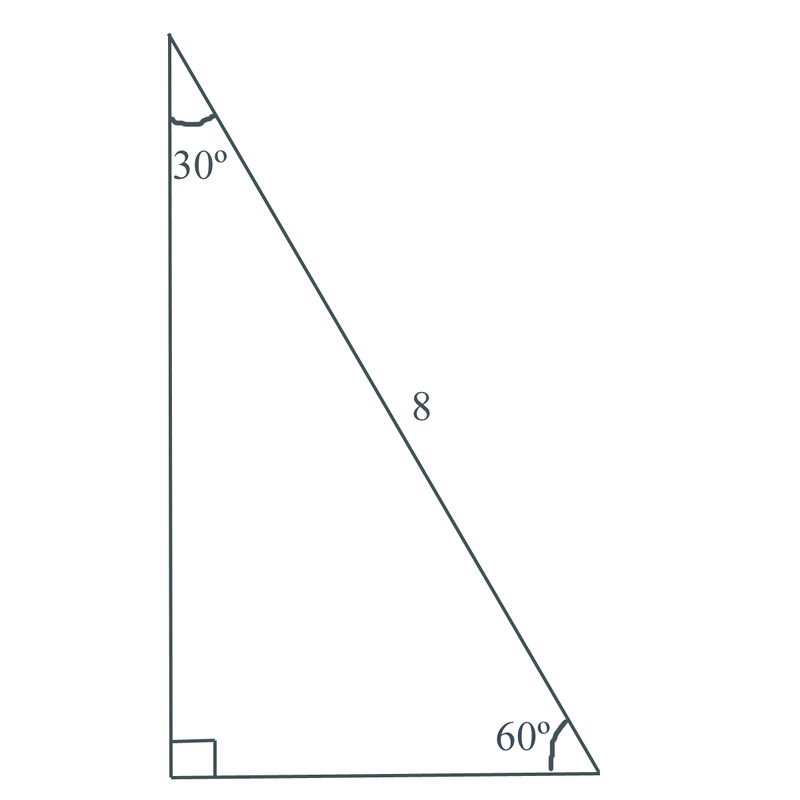
What is the missing angle?
45 degrees
1
What is the acronym we use to remember the basic trig ratios? HINT: sock-uh-toe-uh
*Answer must be spelled correctly*
SOHCAHTOA
1
Set up an equation for sinA
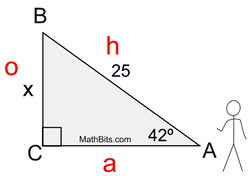
sin42=x/25
1
Which trig function would we use to find the missing angle?
sin-1 (Inverse sine)
1
Write the statement that shows the two smaller triangles are similar
△ JKM ∼ △ KLM
2
What is the name of this type of special triangle?
30-60-90
2
How do we know which side is the hypotenuse?
It' across from the right angle! (Right angle points towards hypotenuse)
2
Set up an equation we could use to solve for y
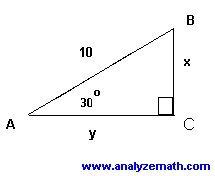
cos30=y/10
2
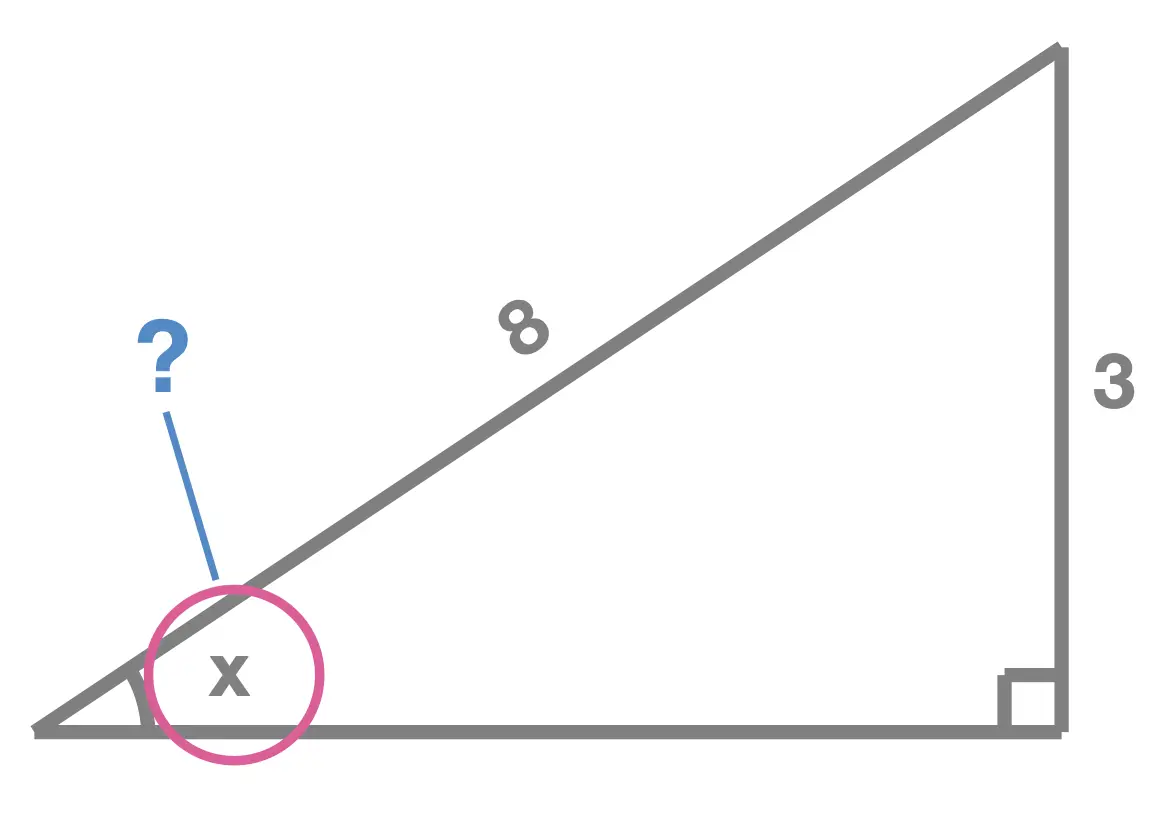
Set up the equation we would use to find the missing angle?
x = sin-1(3/8)
2
Find x
x=4
Solution:
short leg/short leg = long leg/long leg
x/12=12/36
36x=144
x=4
3
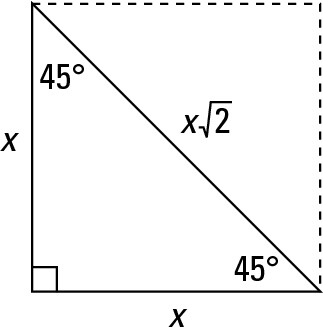
What is the formula to find the hypotenuse in a 45-45-90 degree triangle?
x times the square root of 2
3
Which side is ADJACENT (ADJ) to angle b?
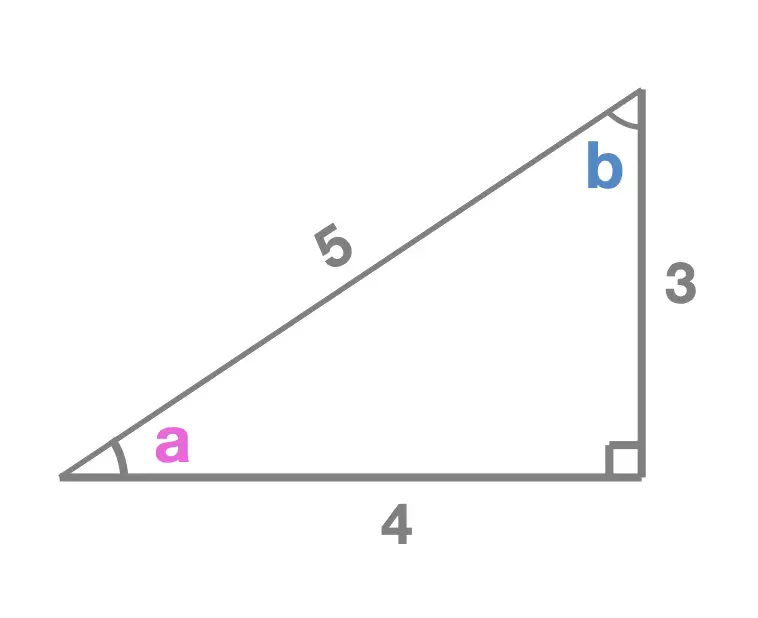
The side with length 3
3
Find b. Round to the nearest whole number!
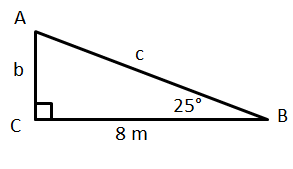
b =4
Solution:
tan25= b/8
8tan25 = b
3.7 = b
Rounding to the nearest whole number, 4=b
3
The missing angle measurement given an opposite side length of 5 and a hypotenuse length of 10.3 (Round to the nearest whole degree)
What is 29 degrees?
3
Let cosA = j and cosA= k. What expression represents the value of sinB - cosB?
j-k
Solution:
Draw your triangle
AB = 1
BC = k
AC = j
sinB = opp/hyp
sinB =j/1
sinB = j
cosB =adj/hyp
cosB =k/1
cosB = k
Thus, sinB - cosB = j - k
4
What is the formula for finding the hypotenuse in a 30-60-90 degree triangle.
2x (two times x)
4
Find cosX
cosX= 4/5
4
Find the missing opposite side length given an angle of 53 degrees and a hypotenuse of length 2.5 (Round to the nearest whole number.)
OPP=2
Solution:
sin=opp/hyp
sin53=OPP/2.5
2.5sin53=OPP
1.99 = OPP
Rounding to the nearest whole number, 2=OPP
4
Find the two angle measurements given the same side lengths of 3.
Both angles are 45 degrees!
This is a 45-45-90 triangle
4
A lighthouse shines its light on a boat from a distance of 3600 meters at an 27 degree angle of depression. Approximately what is the vertical distance from the top of the lighthouse to the sea? (Round to the nearest whole number)
HINT: Find CB
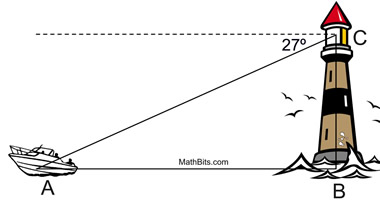
1,634 meters
Solution:
sin27=CB/3600
3600sin27=CB
1634.3=CB
Rounding to the nearest whole number, 1634=CB
5
Find b and c
b=5 times square root 3
c= 10
5
If cosβ =4/5 , what is sinα ?
sinα =4/5
Solution:
sinβ=cosα
cosβ=sinα
By the identity of sine and cosine of complementary angles
5
Find the missing adjacent side length given an angle of 41 degrees and a hypotenuse length of 7. (Round to the nearest whole number.)
ADJ= 5
Solution:
cos= adj/hyp
cos41 =ADJ/7
7cos41 = ADJ
5.2 = ADJ
Rounding to the nearest whole number, 5=ADJ
5
Find the m∠ B. (Round to the nearest whole number)
m∠ B = 56
Solution:
cosB=10/18
B=cos-1(10/18)
B=56.2
Rounding to the nearest whole number, B=56
5
A lighthouse shines its light on a boat from a distance of 3600 meters at an 27 degree angle of depression. Approximately what is the horizontal distance from the boat to the base of the lighthouse? (Round to the nearest whole number)
HINT: Find AB
3,208 meters
Solution:
cos27=AB/3600
3600cos27=AB
3207.6=AB
Rounding to the nearest whole number, 3208=AB