Vocabulary
Translation
Reflection and Rotation
Transformations
Dilation
100
Spin the shape
rotation
100
What is another word for Translation?
Slide
100
Reflect the point (14, 14) across the x-axis. What are the coordinates?
(14, -14)
100
What transformations take Triangle A to Triangle C?
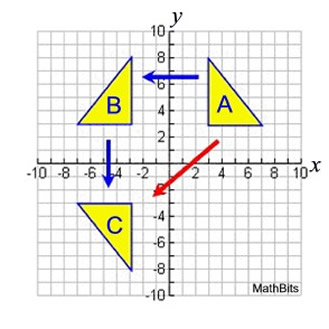
Reflection over y-axis, THEN reflection over x-axis
100
True or False: Dilation is increasing or decreasing the size of the shape
True
200
Two or more lines that never intersect
What is parallel lines
200
What directions help do a translation?
Direction left/right and direction up/down or diagonal
200
Reflect the point (2, 1) across the y-axis. What are the coordinates?
(-2, 1)
200
What sequence of transformations takes you from shape 1 to shape 3?
Rotation 90 degrees counter-clockwise THEN reflection over y-axis
200
A dilation might change the size of a figure's side lengths but never the _______.
angles or shape
300
Slide the shape to a different place
translation
300
Translate the point (3, 2) up 4 units and left 8 units. What are the coordinates?
(-5, 6)
300
If I have a shape in Quadrant 2 and rotate it 180 degrees, what quadrant will it be in?
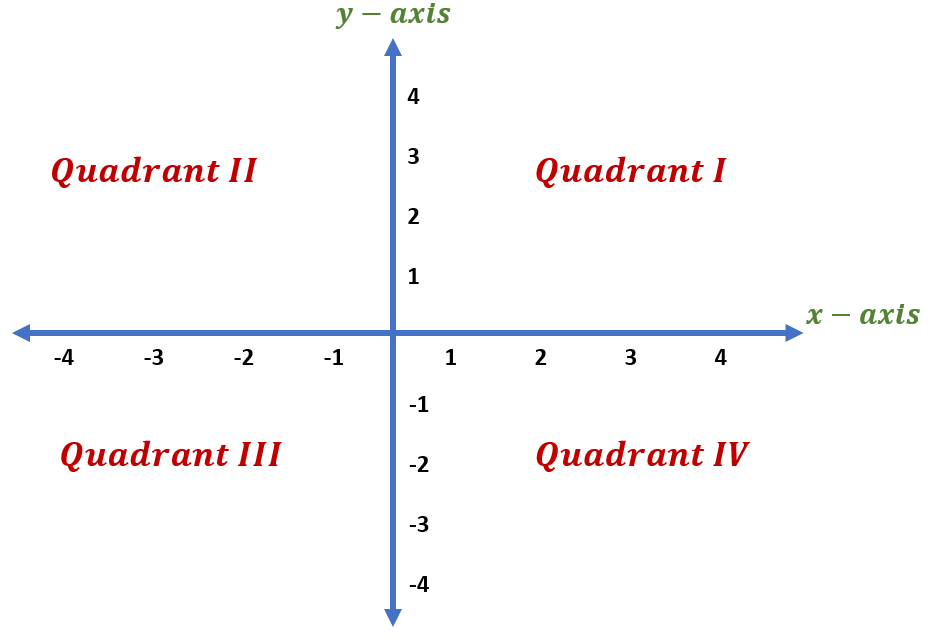
Quadrant 4
300
What sequence of transformations takes you from SRQPT to S"R"Q"P"T"?
Rotate 90 degrees clockwise, THEN reflect across x-axis
300
Dilations always produce ___________ figures.
Similar
400
Flip the shape, mirror image
Reflection
400
Translate the point (3, 2) down 2 units and right 4 units. What are the coordinates?
(7, 0)
400
Reflect the point (2, 1) across the x-axis. What are the coordinates?
(2, -1)
400
This transformation will cause the size to change
Dilation
400
Is a dilation of 7/5 an enlargement or reduction?
Enlargement
500
A type of math that involves shapes and angles.
Geometry
500
Translate the point (-4, -7) up 14 units and right 9 units. What are the coordinates?
(5, 7)
500
If I have a shape in quadrant 1 and I rotate it 270 degrees clockwise, what quadrant am I in?
Quadrant 2
500
What is the sequence of transformations that takes ABC (Blue) to A"B"C" (green)?
(HINT: Orange is the middle step, there are two transformations required to get from blue to green)
Reflection across y-axis
Translation down 5 and left 2
500
If a square is dilated using a scale factor of 2, how many times larger will the area of the new square be?
4 times larger