Reflect over the line
y=-x
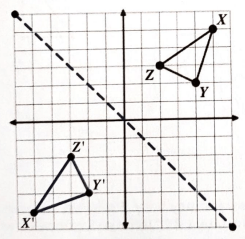
Reflect over the y-axis.
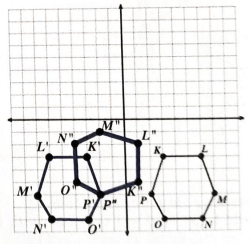
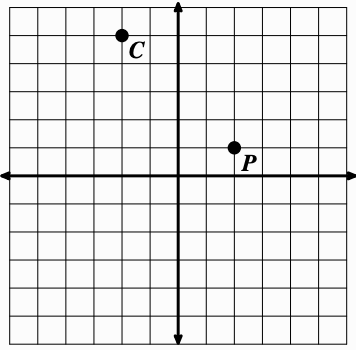
Rotate point P 90º clockwise around point C.
What angles of rotational symmetry are there for a regular pentagon?
Multiples of 72° (72, 144, 216, 288, 360)
Reflect triangle ABC over the line:
y=x
and label the image A'B'C'
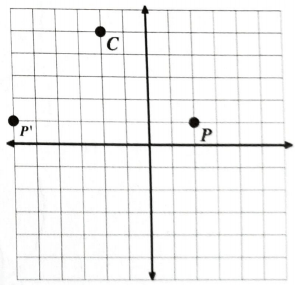
Reflect over the y-axis and then rotate clockwise 90° around P'
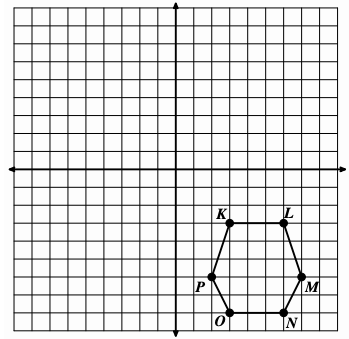
What angles of rotational symmetry are there for a regular hexagon?
Multiples of 60° (60, 120, 180, 240, 300, 360)
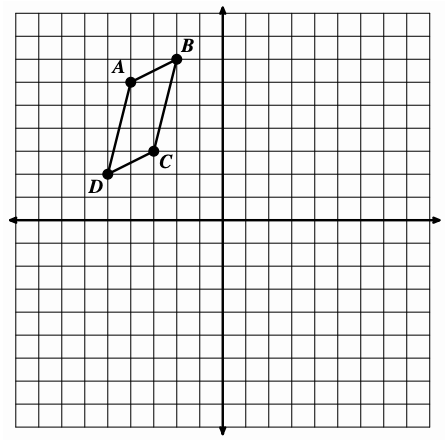
Reflect quadrilateral ABCD over the line:
y=2+x
and label the image A'B'C'D'
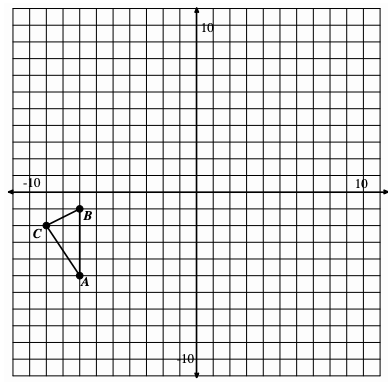
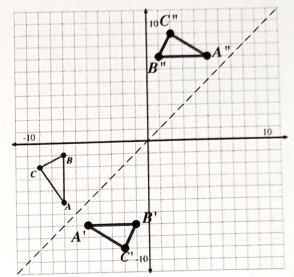
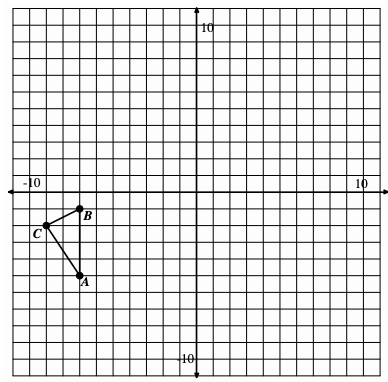
Reflect triangle ABC over the line:
y=x
and label the image A'B'C'.
Rotate A'B'C' 180° counter-clockwise around the origin and label the image A''B''C''
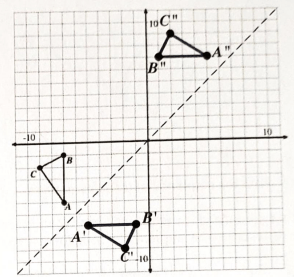
Find a sequence of transformations that will carry triangle RST onto triangle R’S’T’. Clearly describe the sequence of transformations.
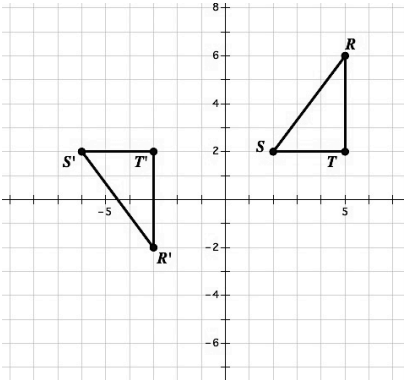
Possible answer:
Translate left 8 so S coincides with S'
Reflect across S'T' so R lands on R'
If a regular polygon has an angle of rotational symmetry that is 40°, how many sides does the polygon have?
9 sides
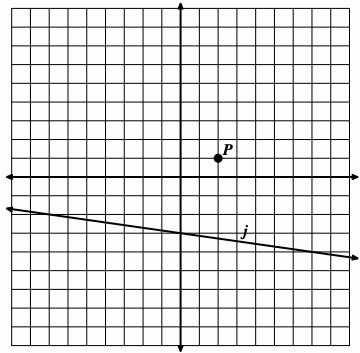
Reflect point P over line j.
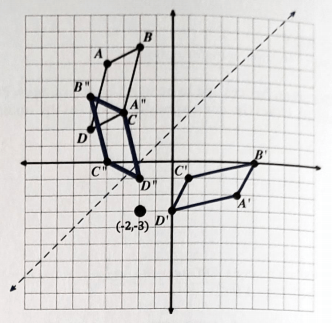
Reflect quadrilateral ABCD over the line:
y=2+x
and label the image A'B'C'D'.
Rotate quadrilateral A'B'C'D' counter-clockwise 90° around (-2, -3) as the center of rotation and label the image A''B''C''D''.

Find a sequence of transformations that will carry triangle RST onto triangle R’S’T’. Clearly describe the sequence of transformations.
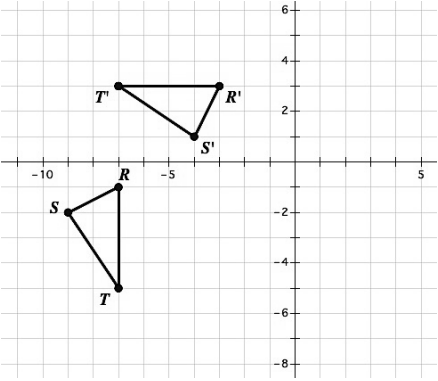
Possible answer:
Translate up 8 units so T coincides with T'
Rotate clockwise 90° about T' until TR coincides with T'R'
Reflect across T'R' so S lands on S'