Translations
Rotations
Reflections
Test Review
Random Facts
100
What is a translation in geometry?
A figure that moves in the same direction and the same distance on a coordinate plane.
100
What is a rotation in geometry?
When a figure turns around a center of rotation.
100
What is a reflection in geometry?
A figure that flips over a line of reflection.
100
A reflection over the line y = x does what to the coordinates: (x,y)
(y, x) It swaps the position of the coordinates.
100
True or false: Sharks existed before trees.
200
How do you translate a point A(2, 3) by 3 units to the right and 2 units down?
(2, 3) --> (x + 3, y - 2)
200
Define the center of rotation.
The point in the middle of a rotation.
200
What are the properties of a shape after it is reflected over the x-axis?
The same side lengths and same angles.
200
List the types of transformations that can be combined in a sequence.
Translation, Reflection, Rotation
200
True or false: A circle has infinitely many lines of symmetry, while a square only has 4.
True!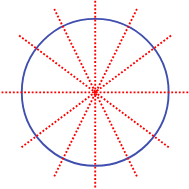
300
Describe the effect of translating a shape on its size and orientation.
The size doesn't change. The orientation does change.
300
If a point B(4, 2) is rotated 900 clockwise about the origin, what are the new coordinates?
2, -4
300
If point C(3, 4) is reflected over the y - axis, what are the new coordinates?
(-3,4)
300
What happens to the coordinates of a translation from (-1, 2) to (7, 4)
The coordinates of the translation become (x,y) --> (x+8,y-6).
300
How old is the Pythagorean Theorem? (Closest gets the points)
2,500 years old!
400
If a triangle has vertices at A(1, 1), B(2, 3), and C(3, 1), what are the new coordinates after a translation of (x + 4, y - 2)?
A (5, -1) B (6, 1) C (7, -1)
400
How does the angle of rotation affect the position of a shape?
The angle of rotation determines which direction a figure is rotated.
400
How do reflections affect the orientation of a shape?
A reflection changes the shapes orientation by flipping the shape over a line of reflection.
400
What transformation is this? (Be Specific)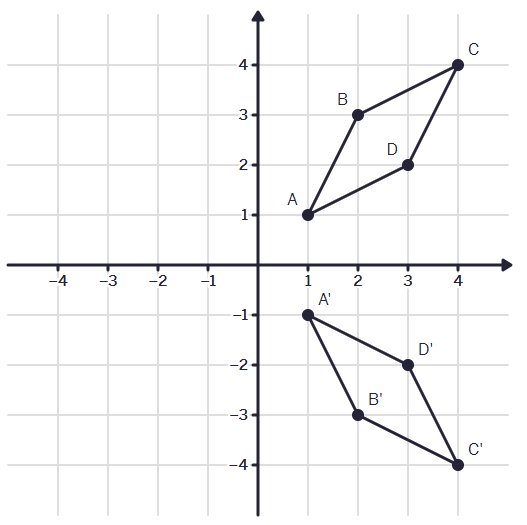
Reflection across the x-axis
400
Which U.S. state is the only one with a one-syllable name?
Maine!
500
Explain how to write the rule when doing a translation.
(x, y) --> x -- add to go right subtract to go left / y -- add to go up subtract to go down
500
Rotate a triangle with vertices at A(0, 0), B(0, 2), and C(2, 0) by 1800 around the origin. What are the coordinates.
A (0, 0) B (0, -2) C (-2, 0)
500
Describe the process of reflecting a triangle over the y-axis.
A triangle reverses its direction of orientation. The x in the coordinates of its verticies become the opposite sign of its original verticies.
500
What transformation is this? (Be specific)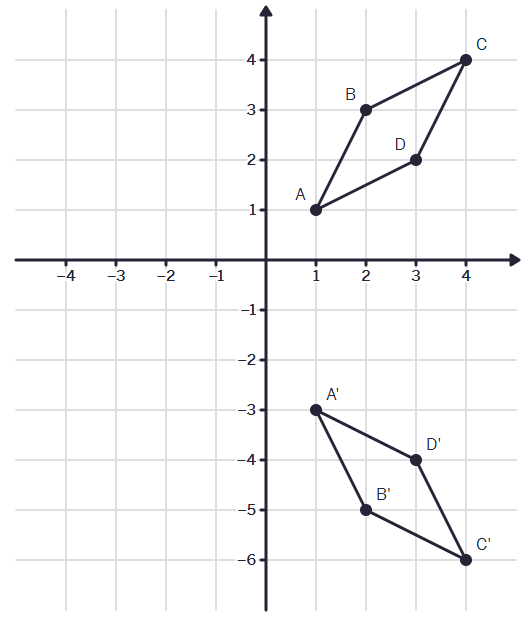
Reflection across the x-axis and a translation of (x, y-2)
500
This shape is called “the roundest object in the universe,” since planets and stars naturally form into it.
A sphere!