LEVEL I
LEVEL II
LEVEL III
LEVEL IV
LEVEL V
100
A __________ is another name for a rotation.
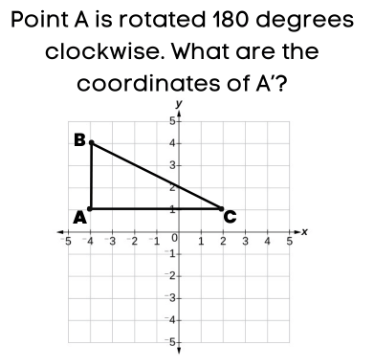
Turn
100
(4, -1)
100
Describe the rotation that has occurred:
(-1,1) → (-1,1)
A 360 degree rotation.
100
The point G(–5,–1)is rotated 180° counterclockwise around the origin. What are the coordinates of the resulting point, G'?
G' is (5, 1).
100
Another term for a 180 degree rotation is a _________.
Half Rotation
200
Which direction is shown?
Counter Clockwise
200
When you rotate 360 degrees does it matter the direction you go in? Explain why or why not.
No, either direction you go the image will end up in the same place as the pre image.
200
Describe the rotation that has occurred:
(1,1) → (-1,-1)
A 180 degree rotation.
200
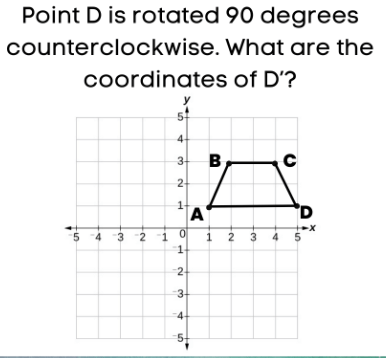
D' is (-1, 5)
200
True or False: A 90 degree clockwise rotation is the same as a 270 degree counterclockwise rotation.
True
300
Each quadrant is _______ degrees.
90
300
How many degrees was the figure rotated? DOUBLE POINTS IF YOU CAN GIVE TWO ANSWERS.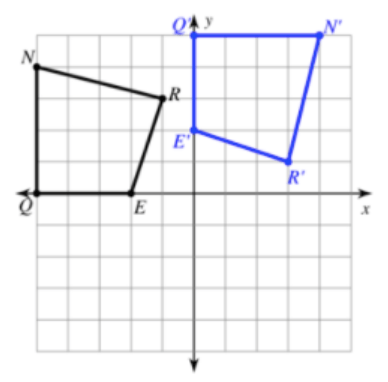
90 degrees clockwise or 270 degrees counter clockwise.
300
Rectangle A is rotated using the rule (x,Y) → (-x,-y). What quadrant will A' be located in?
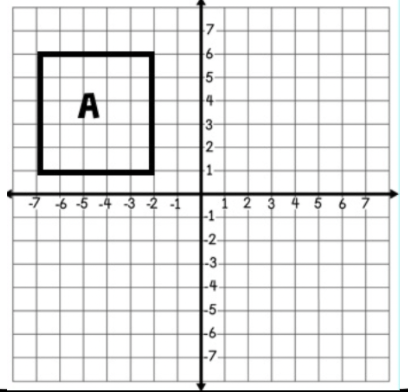
Quadrant IV.
300
Triangle A is rotated 270° counterclockwise with the origin as the center of rotation to create a new figure. Which rule describes rotating 270° counterclockwise?
DOUBLE JEOPARDY!
(x,y)→(y, -x)
300
Write the algebraic notation for a 270 clockwise rotation.
(x,y) ------> (-y, x)
400
In a rotation the pre-image and the image are __________.
Congruent
400
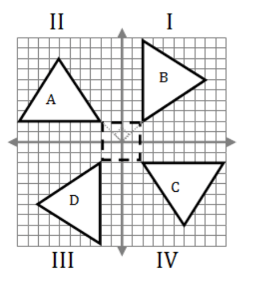
Identify the transformation from A to D.
90 degree Clockwise Rotation
400
What is the angle of rotation for this counterclockwise rotation about the origin?
270 degrees
400
Rotate the point (7,8) around the origin 90 degrees counterclockwise.
State the image of the point.
(-8,7)
400
Write the algebraic notation for rotating 90 degrees counter clockwise.
(x,y) -------> (-y, x)
500
Another term for a 270° turn is a ________.
Three quarter turn.
500
If you were to rotate ABCD 90° counterclockwise about the origin, what would the coordinate of A' be?
DOUBLE JEOPARDY!
(-5, 3)
500
Triangle C is rotated 180° clockwise with the origin as the center of rotation to create a new figure. Which triangle shows the new location?
Triangle A
500
The point C(4,5) is rotated 270° counterclockwise around the origin. What are the coordinates of the resulting point, C'?
C' IS (5,-4)
500
Ava had to determine the coordinates for C' after rotating 90 degrees counter clockwise. She said C' would be located at (0,-3). Her answer was incorrect. Determine the mistake that was made and what the coordinates of C' should be.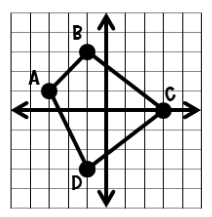
DOUBLE JEOPARDY!
Ava rotated clockwise instead of counter clockwise. The correct coordinates would be (0,3).