GEOMETRY
ALGEBRA II
WORD PROBLEMS
ARITHMETIC & ALGEBRA I
MISCELLANEOUS
100
What is the perimeter of a square that has an area of 25?
20
100
If x-2 = 64, what is the value of x(1/3) + x0?
(Hint: Fraction rules x-2 = 1/x2 & you can change 64 into 25 .)
3/2
100
If 1/3 of a number is 4 less than 1/2 of the number, the number is
24.
Let x represent the unknown number. Since 1/3 of x is 4 less than 1/2 of x, x/3 = x/2 - 4. So, 2x = 3x - 24, giving x = 24.
100
If (23)2 = 4p, then 3p =
Hint:(Use your fraction rules)
27
100
In how many different ways can five students be seated in three chairs?
60.
5x4x3=60
200
What is the circumference of a circle in which a 5 by 12 rectangle is inscribed?
(Hint: C = 2(pi)r )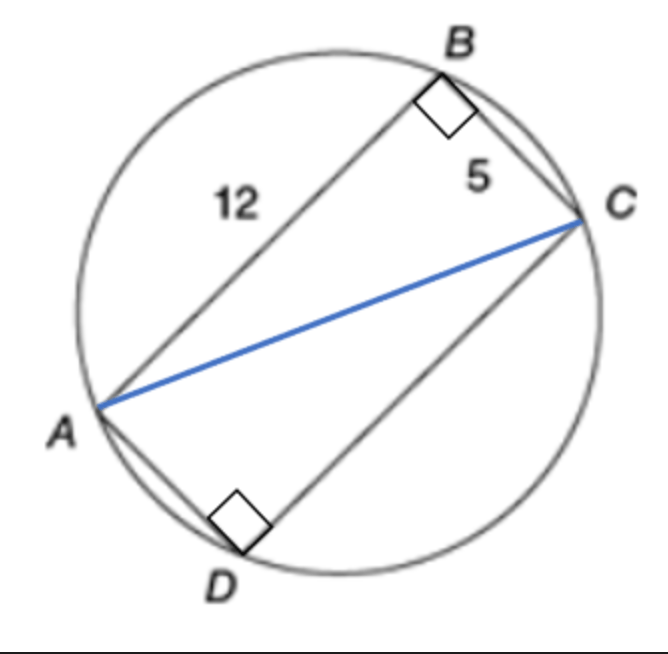
13pi. The length of a diagonal of a 5 by 12 rectangle is 13 (pythagorean theorem). The diagonal of the rectangle is the diameter of the circle inscribed, and C = 2(pi)r.
200
Which of the following is the graph of the equation y=2x-5 in the xy-plane?
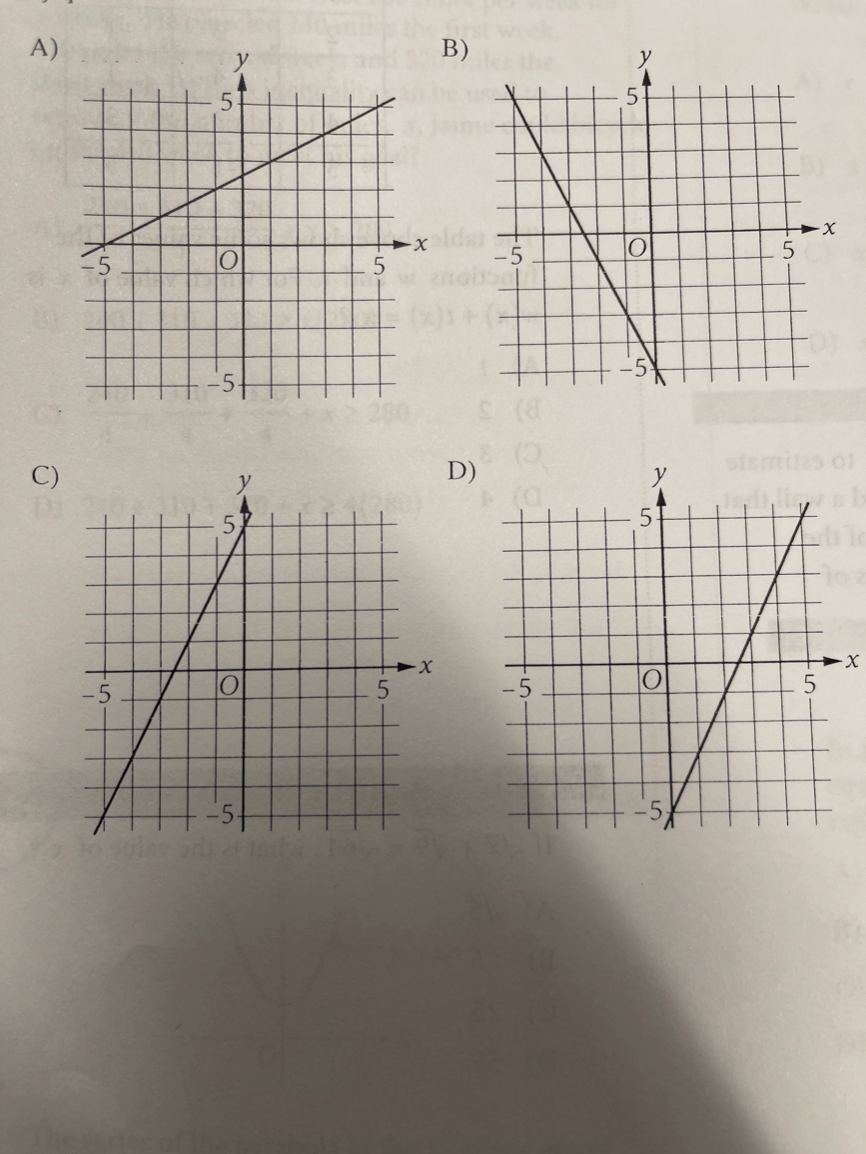
The correct Answer is D.
200
A school district is forming a committee to discuss plans for the construction of a new high school. Of those invited to join the committee, 15% are parents of students, 45% are teachers from the current high school, 25% are school and district administrators, and the remaining 6 individuals are students. How many more teachers were invited to join the committee than school and district administrators?
The correct answer is 8.
The 6 students represent (100 − 15 − 45 − 25)% = 15% of those invited to join the committee.
If x people were invited to join the committee, then 0.15x = 6. Thus, there were 6/(0.15)=40 people invited to join the committee. It follows that there were 0.45(40) 0.15= 18 teachers and 0.25(40) = 10 school and district administrators invited to join the committee.
Therefore, there were 8 more teachers than school and district administrators invited to join the committee.
200
When the number of people who contribute equally to a gift decreases from four to three, each person must pay an additional $10. What is the cost of the gift?
$120.
200
What is the area of the circle whose radius is the average of the radii of two circles with areas of 16pi and 100pi?
49pi.
300
The height h of a cylinder equals the circumference of the cylinder. In terms of h, what is the volume of the cylinder?
Hint:(V = pi(r2 )h)
(h^3)/4pi. h=2(pi)r, so r=h/2pi.
Volume of cylinder = pi(r^2)h = pi[(h/2pi)^2]h = (h3)/4pi
300
A culture of 5000 bacteria triples every 15 minutes. What is the size of the bacteria population after 2 hours have elapsed?
32,805,000
300
The regular price of software at a computer superstore is 12% off the retail price. During an annual sale, the same software is 25% off the regular price. If the retail price is p, what is the sale price in terms of p?
Hint: ( "in terms of " means to solve for one variable and use the expression to write with only one or more variables that are given)
0.66p. Since the regular price of software is 12% off the retail price p, the regular price of the software can be expressed as 0.88p. So the sale price is 0.75 x 0.88p = 0.66p.
300
Simplify (4a+a-3)(4b-2b-b)
5ab-3b
300
Three fair coins are tossed at the same time. What is the probability that all three coins will come up heads OR all will come up tails?
1/4.
1/8 (all heads) + 1/8 (all tails) = 1/4.
400
If the integer lengths of the three sides of a triangle are 4, x, and 9, what is the least possible perimeter of the triangle?
19.
In the given triangle, 9-4
400
What is the equation of the graph obtained by shifting the graph of y=x^2 horizontally to the left 4 units and vertically down 3 units?
y = (x+4)^2 - 3
400
Jars A, B, and C each contain 8 marbles. What is the minimum number of marbles that must be transferred among the jars so that the ratio of the number of marbles in jar A to the number in jar B to the number in jar C is 1:2:3?
4. Since jars A, B, and C each contain 8 marbles, there are 24 marbles in the three jars. Let x, 2x, and 3x represent the new numbers of marbles in jars A, B, and C, respectively. Hence, x + 2x + 3x = 24 or 6x = 24, so x=4.
400
For the system of three equations:
x-z=7, x+y=3, z-y=6, what is x?
8
400
Five students, all of different heights, are randomly arranged in a line. What is the probability that the tallest student will be first in line and the shortest student will be last in line?
1/20.
1x3x2x1x1=6, 6 ways in which students can be arranged under given conditions. Under no conditions, the ways are 5x4x3x2x1=120. 6/120=1/20.
500
Triangles ABC and DEF are shown above. Which of the following is equal to the ratio (BC)/(AB)?
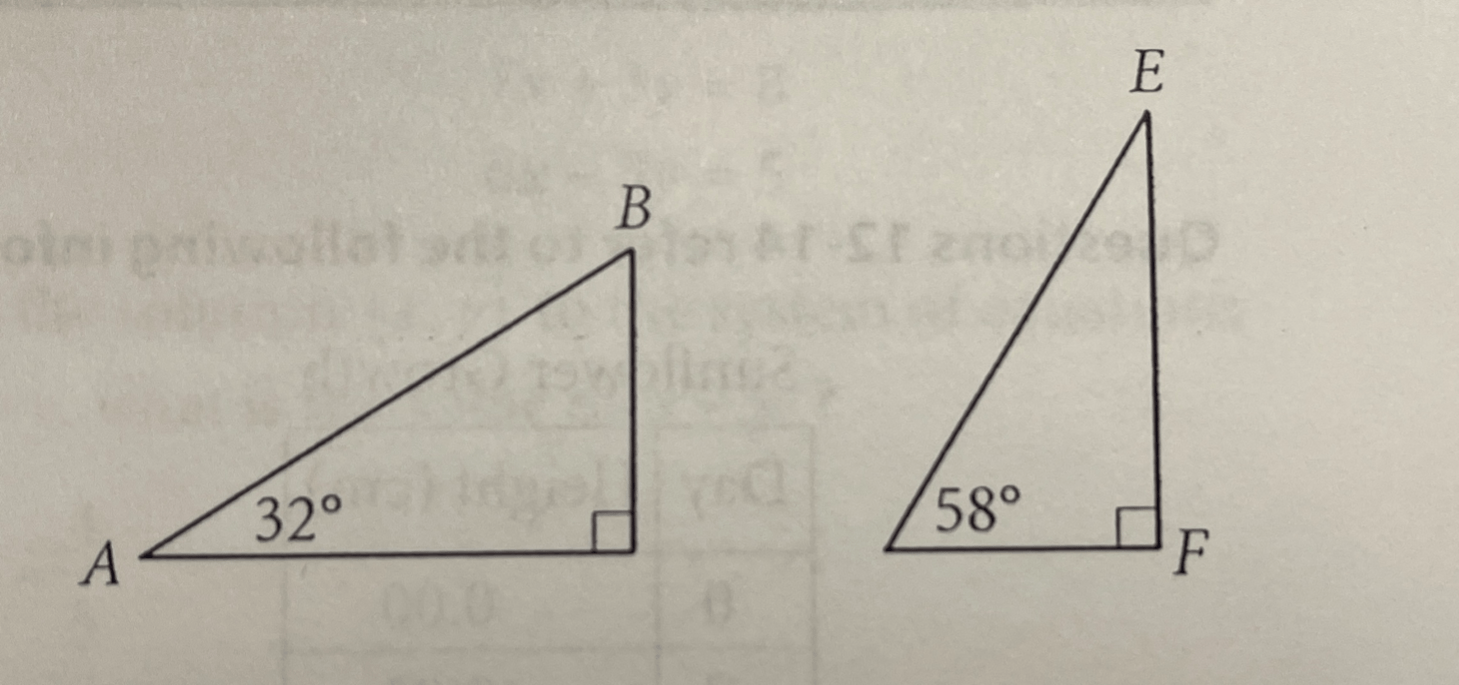
Choice B is correct. In right triangle, ABC, the measure of angle B must be 58° because the sum of the measure of angle A, which is 32°, and the measure of angle B is 90°. Angle D in the right triangle DEF measures 58°. Proving that triangles ABC and DEF are similar. Since BC is the side opposite to the angle with measure 32° and AB is the hypotenuse in right triangle ABC, the ratio (BC)/(AB) = (DF)/DE).
500
If x = (2/3)y and y = 18, what is the value of 2x-3?
A)21
B)15
C)12
D)10
The correct answer is A.
Substituting the given value of y = 18 into the equation x = (2/3)y. x = (2/3)(18), and x = 12. The value of the expression 2x − 3 when x = 12 is 2(12) − 3 = 21.
500
Fruit for a dessert costs $1.20 a pound. If 5 pounds of fruit are needed to make a dessert that serves 18 people, what is the cost of the fruit needed to make enough of the same dessert to serve 24 people?
Hint: Solve for x (5/18) = (x/24).
$8.00. If 5 pounds of fruit serve 18 people, then 5/18 pound serves one person, so 24 x 5/18 = 20/3 pounds. Since the fruit costs $1.20 a pound, the cost of the fruit needed to serve 24 people is 20/3 x $1.20 = $8.00.
500
A bricklayer uses the formula n= 7lh to estimate the number of bricks, n, needed to build a wall that is l feet long and h feet high. Which of the following correctly expresses l in terms of n and h?
Hint: ( "in terms of " means to solve for one variable and use the expression to write with only one or more variables that are given) in this case you are solving for l.
l = (n/7h)
500
x, y, 22, 14, 10... In this sequence, each term after the first term x is obtained by halving the term that comes before it and then adding 3 to that number. What is the value of x-y?
32.
x=70, y=38. 70-38=32.