Lines of Best Fit
Independent Events
Dependent Events
Relative Frequency
100
Where should a line of best fit be drawn?
a) In the middle of the data with half above and half below the line
b) Connecting each data point by passing through each point
a) In the middle of the data with half above and half below the line
100
You flip a coin twice. What is the probability of getting heads twice?
Express your answer as a simplified fraction.
1/4
100
A bag has four blue marbles and five red marbles. What is the probability of getting two blue marbles, without replacement?
Express your answer as a simplified fraction.
1/6
100
The 30 students in a class did a survey of how many pets each of them owned and recorded the results as follows: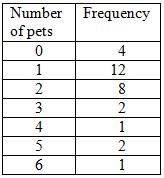
What was the relative frequency for a student either owning one pet or owning two pets?
(You may use a calculator)
0.667
12 students out of 30 said they owned one pet and 8 said they owned two pets.
12 + 8 = 20
So the relative frequency was 20/30 = 2/3 = 0.667
200
What is the first step when finding a line of best fit?
a) Find two data points that are closest to the line.
b) Find two places that the line passes through, whether or not they are data points.
b) Find two places that the line passes through, whether or not they are data points.
200
You roll a number cube twice. What is the probability of getting a two and then a five?
Express your answer as a simplified fraction.
1/36
200
A bag has three white marbles, a yellow marble, and five red marbles. What is the probability of getting two red marbles, without replacement?
Express your answer as a simplified fraction.
2/9
200
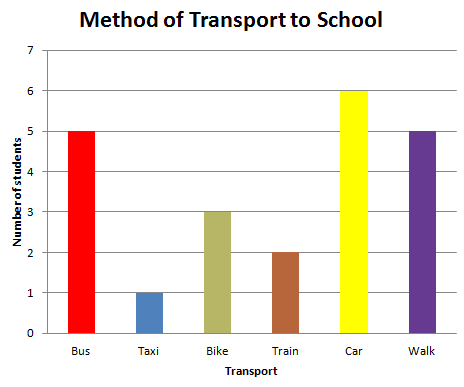
The bar graph shows the usual method of transport to school for the students in a class.
What is the relative frequency for traveling to school by car?
0.27
The total number of students
= 5 + 1 + 3 + 2 + 6 + 5
= 22
Just add up the heights of all the bars.
Of these, 6 students travel to school by car.
So the relative frequency for traveling to school by car = 6/22 = 0.27 (to 2 decimal places).
300
A line of best fit has a positive slope. What does this mean?
a) As x increases, y increases.
b) As x decreases, y increases.
c) As x increases, y decreases.
a) As x increases, y increases.
300
A bag has four blue marbles and five red marbles. What is the probability of getting two blue marbles, with replacement?
Express your answer as a simplified fraction.
16/81
300
A bag has the letters of the word MATHEMATICS in in. What is the probability of drawing two letters and getting an M then a C without replacement?
Express your answer as a simplified fraction.
1/55
300
Jane did a count of the number of times each of the vowels occurred on one page of her book, with the following results: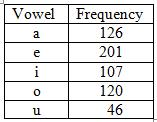
What was the relative frequency of the vowel a?
0.21
First find the total number of vowels on the page
= 126 + 201 + 107 + 120 + 46
= 600
There were 126 a's out of 600 vowels altogether.
So the relative frequency of the vowel a = 126/600 = 63/300 = 21/100 = 0.21
400
A line of best fit has a negative slope. What does this mean?
a) As x increases, y increases.
b) As x decreases, y decreases.
c) As x increases, y decreases.
c) As x increases, y decreases.
400
You flip a coin twice. What is the probability of getting two different results (one time heads and one time tails), regardless of order?
Express your answer as a simplified fraction.
1/2
400
A bag has the letters of the word MATHEMATICS in in. What is the probability of drawing two letters and getting two vowels without replacement?
Express your answer as a simplified fraction.
6/55
400
A die was thrown 60 times with the following results: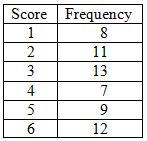
What was the relative frequency for a score of six?
0.2
Six occurred 12 times out of 60 throws altogether.
Therefore, the relative frequency for a score of six = 12/60 = 1/5 = 0.2