Name a pair of alternate interior angles.
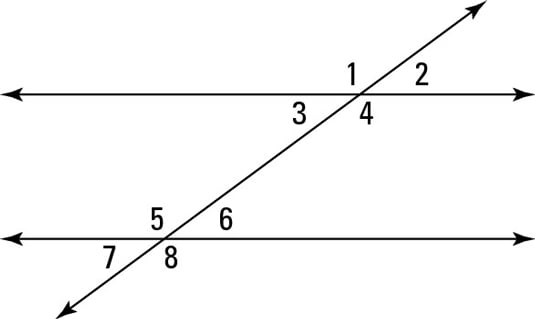
3 and 6 or 4 and 5
Describe the following transformation.

Reflection over the y axis
What slope would parallel to the line y=5x+2?
5
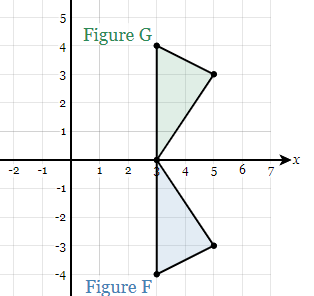
Describe the transformation from G onto F.
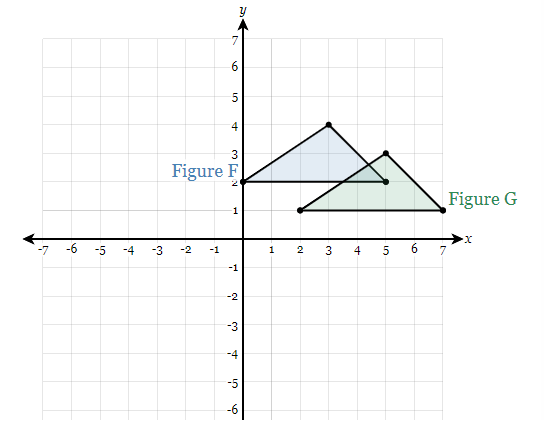
Translation left 2 up 1
What slope would be parallel to 2/3?
2/3
Find x.

110
Describe the following transformation.
Up 3, left 5
What kind of angle pair is 2 and 7?

Alternate exterior
Describe the transformation.
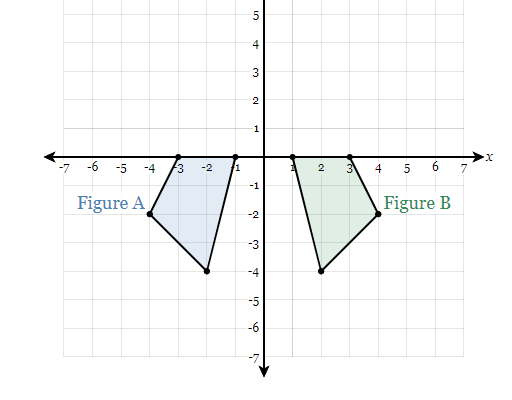
Reflection over the y-axis
What slope would be perpendicular to -6?
1/6
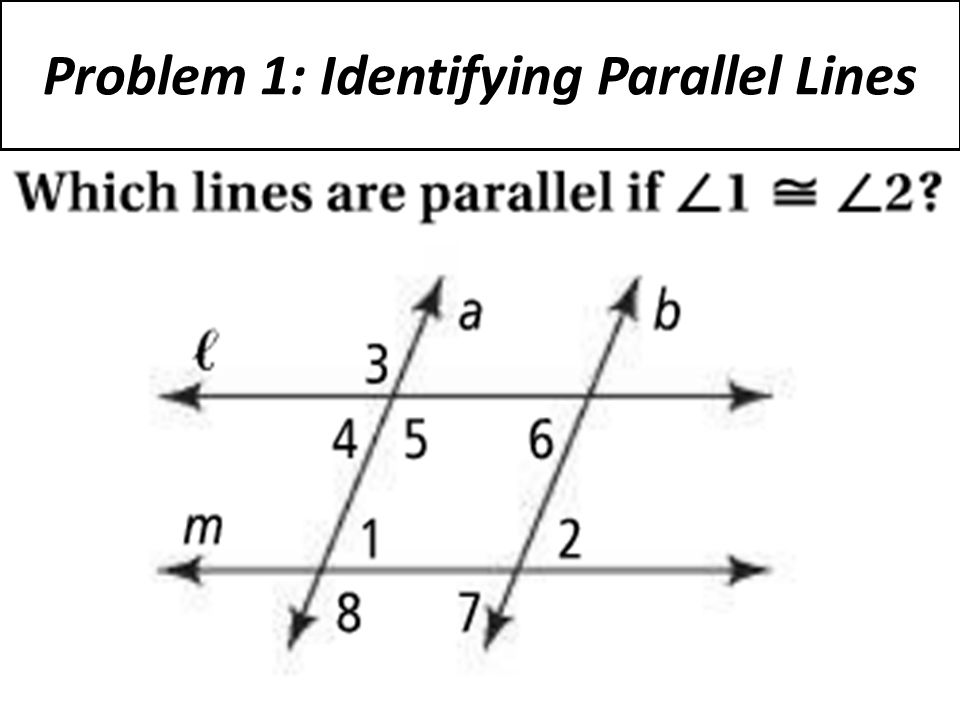
a||b
Describe the transformation.
reflection over the x-axis
Name a pair of corresponding angles.

Many answers
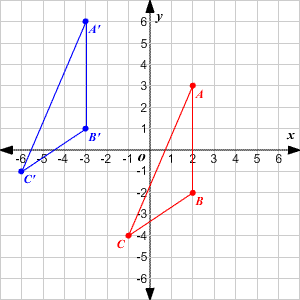
Take the 3 points and translate them right 4, down 3.
A (2,1)
B(4,-2)
C(-3,5)
A'(6,-2)
B'(8,-5)
C'(1,2)
Find the slope of a line perpendicular to the line whose equation is 6x+8y=-128
4/3
Find x.
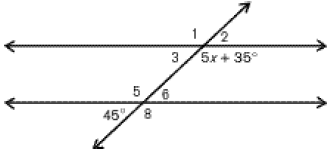
x=20
Describe the transformation.

90 degree rotation clockwise
or
270 degree rotation counterclockwise
If the lines are parallel, why would angle 1 and angle 8 be congruent?

They are alternate exterior angles
What transformation would map figure A onto figure B?
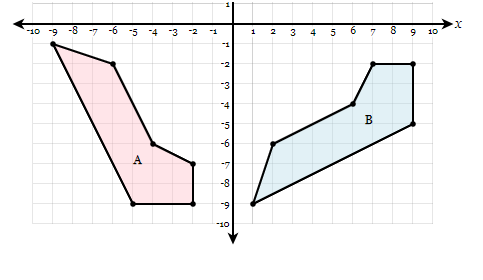
90 degree rotation counterclockwise
Which equation represents a line which is perpendicular to the line 5x+2y=12?
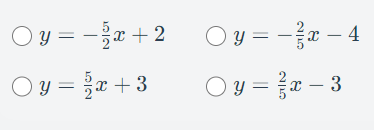
y=2/5x-3
Based on the given information, what two lines would be parallel? angle 4 is congruent to angle 6
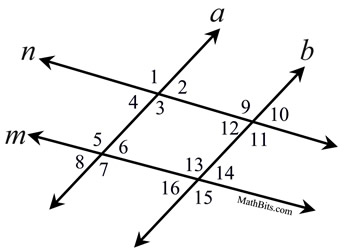
n||m
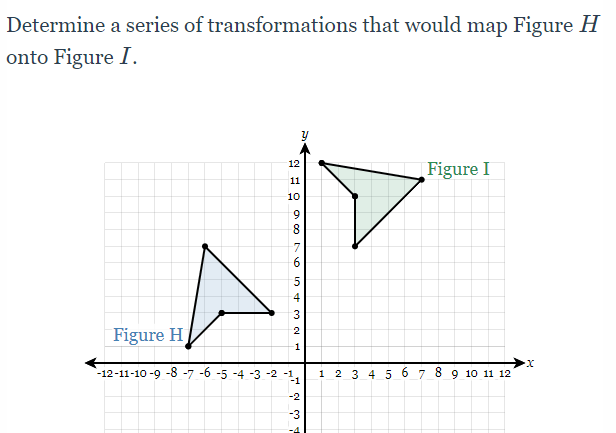
Rotation 270 counterclockwise or 90 degrees clockwise followed by a translation up
y=-1/2x-3
Give 3 possible rotations (in degrees) that would map this figure onto itself.

72, 144, 216, 288, 360

y=-5/4x+14