Polynomials
Conversions
Transformations
Misc
Final Jeopardy
100
What is the degree of the polynomial?
g(x)=(x+5) (x-8)^3
4
100
What is the name of the form shown below?
y=(x+2)(x+8)
Factor Form
100
What is the name of the form shown below?
y=a(x+h)^2-k
Vertex Form
100
Daily Double!
A polynomial with two terms
Binomial
200
What are all the zeros of the polynomial?
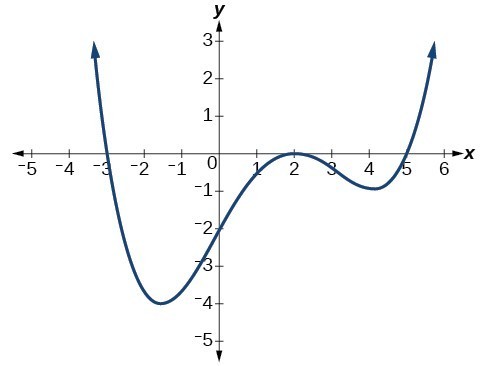
(-3,0) (2,0) (5,0)
200
This equation below is given in standard form, what is the y-intercept?
y=x^2+8x-9
The C term - (0,-9)
200
Which variable is responsible for stretches, compressions and reflections of a graph?
y=a(x+h)-k
a
200
What is the degree of the polynomial?
f(x)= 3x^5+x^3+2x-6
5
300
Draw it!
If we have a polynomial that is positive and has a degree of 5, what shape would the polynomial be?
300
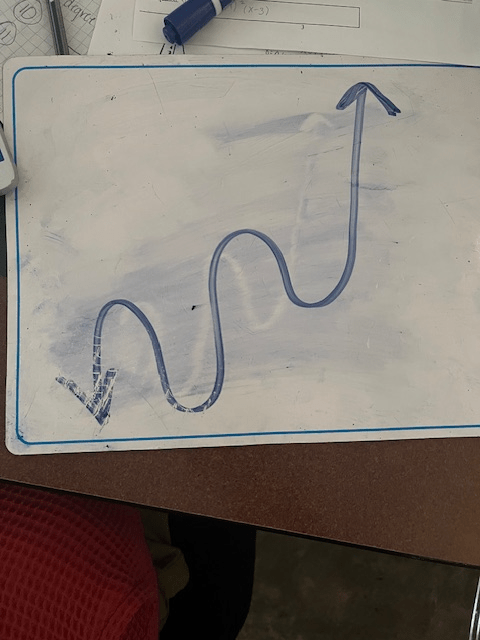
The equation below is given in factor form, what are the x-intercepts?
y=(x-5)(x+7)
(5,0) (-7,0)
300
Daily Double!
The equation below is given in vertex form, what is the vertex?
y=3(x+4)^2-5
(-4,-5)
300
True or False
If the h-value in the equation is positive, the h-value in the vertex is negative.
True, the h-values always switch signs!
300
Write it on the whiteboard!
Find the A-value given a point and an equation.
(5,-14)
y=A (x+2)(x-4)^3
A=-2
400
If a polynomial graph curves through the x- axis, what is the exponent on the factor (x+1)?
f(x)=(x+3)(x+1)^(?)(x-2)^2
3
400
Fill in the blank:
When converting from standard form to factor form, we must find the factors of ___ that add to get to ___.
C, B
400
Write it on the whiteboard!
What is the name of the parent function shown below and what is the equation? Write it on the whiteboard!
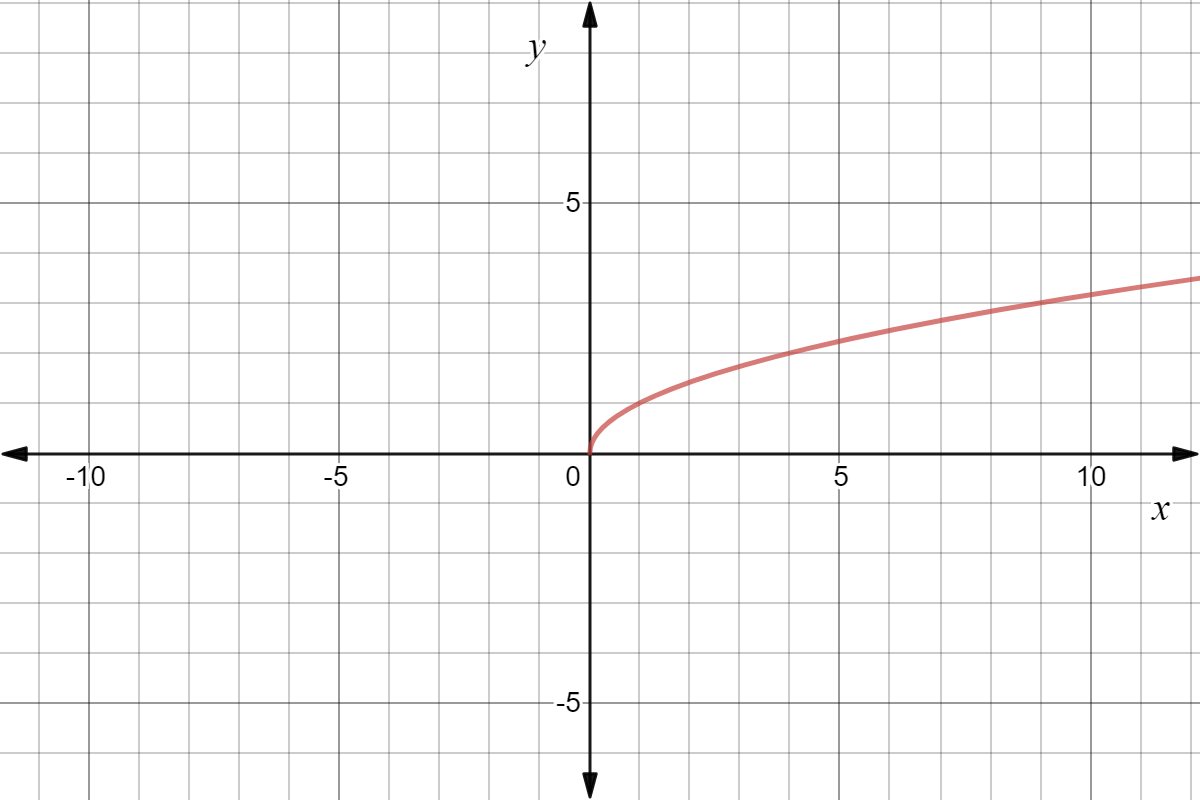
Square Root f(x)=sqrt(x)
400
Write it on the white board!
If I have a linear function with a stretch of 1/3 and moves 6 spaces up, what would be equation look like?
y=1/3x+6
500
Daily Double!
If the graph touches the x-axis and bounces back, does the graph have a single, double, or triple root?
double
500
When converting from standard from to vertex form, what number do you always divide the B term (middle term) by?
2
500
Comparing the red graph to the black graph, describe the transformations of the red graph. 
right 8, negative (a-value/function/equation/graph)
500
Which conversion is NOT possible ?
A. Standard Form to Factor Form (SF---FF)
B. Vertex Form to Standard Form (VF---SF)
C. Factor Form to Vertex Form (FF---VF)
C. Factor Form to Vertex Form, you must convert to Standard Form first!
--------------------------------------------------------
A. Standard Form to Factor Form (SF---FF) uses the area model
B. Vertex Form to Standard Form (VF---SF) uses expanding and distribution