Function Vocabulary
Graphs of Functions
Exponential Functions
Linear Functions
Miscellaneous
100
What is the definition of a function?
A relation between two sets where each value of one set, X (inputs), are paired with one and only one value of the other set, Y (outputs).
100
Evaluate each of the following:
f(-2) = f(8) =
f(-8) = f(4) =
f(-2) = -3
f(-8) = -3
f(8) = 3
f(4) = -1
100
What is the general form for an exponential equation? Label all part of the equation.
y = a(b)x
y = output
x = input
a = initial value
b = multiplier
100
What is the general form for a linear function/equation? Label all parts.
y = mx + b
y = output
x = input
m = slope (repeated addition)
b = x-intercept (initial value)
100
Given the function f(x) = x2, evaluate the following:
f(2)
f(-5)
f(0)
f(2) = 4
f(-5) = 25
f(0) = 0
200
What is the domain of a function?
All possible values of x (inputs) that generate a y (outputs).
200
Consider the function f(x) = x2:
Fill out a function table for the following inputs: x = -3, -2, -1, 0, 1, 2, 3.
Using the table, on what interval is the function increasing? On what interval is it decreasing?
x = -3, y = 9 | x = 1, y = 1
x = -2, y = 4 | x = 2, y = 4
x = -1, y = 1 | x = 3, y = 9
x = 0, y = 0
Increasing: x≥0
Decreasing: x≤0
200
A town currently has 10,000 people. The town's population is declining by 5% each year. Write a function that represents the size of the population, P, after t years.
P(t) = 10,000(.95)t
200
Isaac pays a flat rate plus a rate per minute for his phone plan. He pays a flat rate of $20 plus $0.15 per minute. Write a function that represents Isaac's total cost, C, based on the number of minutes, m, he uses.
C(m) = 0.15m + 20
200
What is the range of y = 2x2 + 1 given a domain of {-2, -1, 0, 1, 2}?
Range: {1, 3, 9}
Since we are given a discrete domain, all we have to do to find the range is plug in each value of the domain and solve for y. Notice, some outputs repeat but we only have to list them once in the range.
300
What is the range of a function?
All possible values of y (outputs) that can be generated by the function (that have an x paired with it).
300
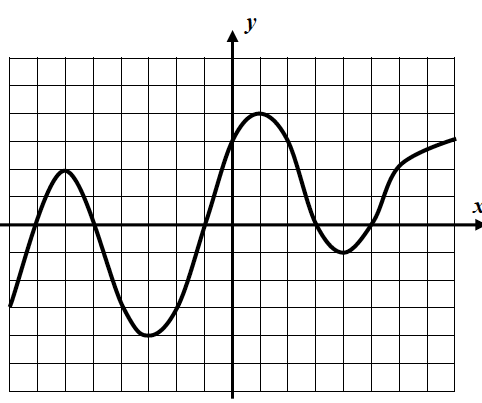
Find all relative maximums and relative minimums.
Relative Maximums: (-1, 7) (5, 5)
Relative Minimums: (-5, -1) (2, 2)
300
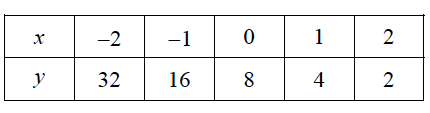1. Does this table represent an exponential or a linear function?
2. Write an equation to represent this table.
1. Exponential because the output (y) is being repeatedly multiplied by some common multiplier.
2. y = 8(1/2)x
300
A construction crew is re-paving Raleigh-Millington Road. They've already paved 2000 square feet and can pave at a rate of 600square feet per hour. The function f(x) = 600x + 2000 represents this situation.
What is f(2) and what does it represent?
f(2) = 600(2) + 2000 = 1200 + 2000 = 3200
f(2) represents the total number of square feet the construction crew has paved after 2 hours.
300
For f(x) = x2 + x, which of the following gives an output of 2?
1) f(2)
2) f(4)
3) f(-2)
4) f(-4)
f(-2)
400
Label each element of the following function notation:
f(x) = y
f(x) = y
f = function rule
x = input
y = output
400
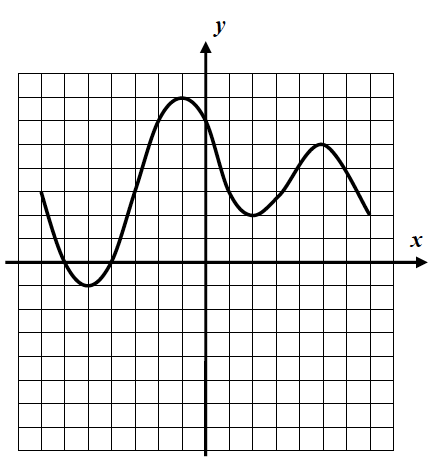
What are the domain and range of the graph?
Domain: x ≤ 5
Range: y ≤ 2
400
Wildlife biologists are tracking a population of deer in a forest preserve. They've tracked the population every year since 2005.
Find a formula to model the total deer population from year to year.
P(t) = 86(1.14)t
400
Thomas and Maya go to the store to buy decorations for a party. Thomas bought 5 packages of balloons (b) and 3 table clothes (t) for $15.77. Maya bought 2 packages of balloons and 7 table clothes for $13.28. What system of equations could be used to solve for the price of balloons and table clothes?
1) 5b + 3t = 13.28
2b + 7t = 15.77
2) 5b + 2t = 15.77
3b + 7t = 13.28
3) 5b + 3t = 15.77
2b + 7t = 13.28
4) 7b + 3t = 13.28
2b + 5t = 15.77
3) 5b + 3t = 15.77
2b + 7t = 13.28
400
The student-to-faculty ratio at the University of Memphis is 15-to-1 meaning there are 15 students for every one faculty member. This can be shown by the function f(x) = 15x where x is the number of faculty and f(x) is the number of students. Which of the following numbers could be part of the domain of this function?
1) -15
2) -3.5
3) 0
4) 5
4) 5
We must consider the context of the problem. Can you have negative faculty members? Can you have a fraction of a faculty member? Is it likely that the University of Memphis has 0 faculty members?
500
Define the following vocabulary words:
1. Relative Maximum
2. Relative Minimum
3. Zeroes of a Function
1. Relative Maximum: Turning point on graph where the graph goes from increasing to decreasing.
2. Relative Minimum: Turning point on graph where the graph goes from decreasing to increasing.
3. Zeroes of a Function: the values of x where y = 0 OR the x-intercepts OR the inputs of a function that result in an output of 0.
500
What are the zero(s) of the following function?
f(x) = 2x + 1
x = -1/2
(Remember, the zero of a function is the x-value of the function when y = 0)
500
Create an explicit formula to model the following geometric sequence: 4, 8, 16, 32, 64, 128, ......
an = 4(2)n-1
500
A warehouse is keeping track of its inventory of cardboard boxes. At the beginning of the month, they had 1,275 boxes left. They use boxes at a rate of 75 per day.
How many boxes are left after 10 days?
f(x) = -75x + 1275
f(10) = -75(10) + 1275
= -750 + 1275
= 525
525 boxes remain after 10 days.
500
A man takes out a $7000 loan for a car. He wants to create a function to help him estimate how much he owes over time as he pays the loan back. He combines the constant function f(t) = 7000 and the linear function g(t) = 550t to create the function h(t) = f(t) - g(t) where h(t) represents the total amount still owed on the loan after t years. How much will he have left to pay off 2 years after taking out the loan?
h(t) = f(t) - g(t)
h(t) = 7000 - 550t
h(2) = 7000 - 550(2)
h(2) = 5900
He will still owe $5900 two years after taking out the loan.