Systems of Equations
Factoring
Matrices
Exponents
Logs
100
Let's solve your system by substitution.
x+y=7
x+2y=11
x=3 and y=4
100
Factor using GCF(Greatest Common Factor)
A: 16p4 +4p3
4p3(4p + 1)
100
Solve by using Addition: 3x2
[3 6] [0 -1]
[-1 -3] + [6 0] =
[-5 -1] [2 3]
A: 3x2
[3 5]
[5-3]
[-3 2]
100
Laws of Exponents Product Rule:
x3 * x8 =
A:
x11
100
log x(8) =1/3
x=512
200
Use elimination to solve for x and y.
4x + 2y = 14
5x + 2y = 16
The solution is (2, 3).
200
Factor Using Difference Of Squares:
A: 36k2 −1
(6k+1)(6k−1)
200
Solve Using Inverse:2x2
[11 -5]
[2 -1]
A:2x2
[1 -5]
[2 -11]
200
Simplify:
x5 * x3 =
A:x8
200
log2(64) = x-4
x=10
300
Solve for x and y.
-x – y = -4
x + y = 2
-x – y = -4
x + y = 2
0 = −2
Add the equations to eliminate the
x-term.
Answer
There is no solution.
300
Factor the Trinomial:
A: n2 −n−56
(n + 7)(n − 8)
300
find the determinant of this 2x2:
[-1 1]
[-1 4]
A: -3
300
Solve:
43/2=
A: 8
300
(1/7)^x=7^x+4
x=-2
400
Solve for x and y.
x + y = 2
-x − y = -2
x + y = 2
-x − y = -2
0 = 0
Add the equations to eliminate the
x-term.
Answer
There are an infinite number of solutions.
400
Factor Using the AC Method:
A: 10x2 -3x-1
(5x+1)(2x−1)
400
Solve Using Inverse of Matrices:
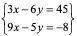
A:
400
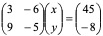
Compound Interest: hint: A = P (1 + r/n)(nt)
You borrowed $59,000 for 2 years at 11% which was compounded annually. What total will you pay back?
A: $72,693.90
400
e^In(2.5)
2.5
500
Use elimination to solve the system.
x – y = −6
x + y = 8
2x = 2
x = 1
Solve for x.
x + y = 8
1 + y = 8
y = 8 – 1
y = 7
Substitute x = 1 into one of the original equations and solve for y.
x – y = −6
1 – 7 = −6
−6 = −6
The solution is (1, 7).
500
Factor by Grouping:
A: 140ab−60a2 +168b−72a
4(5a + 6)(7b − 3a)
500
Use RREF To solve the system:
{3x+4y=11}
{2x-5y=-8}
HINT:[3 4 11]
[2 -5 -8]
A: [1 0 1]
[0 1 2]
500
Compound Interest: hint: A = P (1 + r/n)(nt)
Your $440 gets 5.8% compounded annually for 8 years. What will your $440. be worth in 8 years?
A: $690.78
500
"Thor spent $12,125 on a credit card with 12.5% annual percentage interest rate compounded continuously. he makes no payments for 2 years. How much does he own then?
A=15568.80