What is a ratio?
A ratio is a comparison of two quantities.
What is a proportion?
Two ratios that equal each other.
Find the missing side length: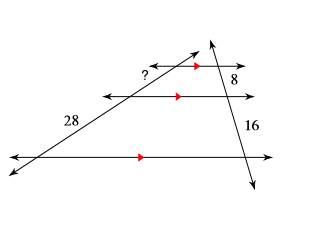
? = 14
Find x:

x = 3
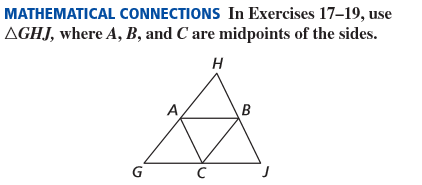
A midsegment of a triangle is a line segment that connects the ____________ of two sides of a triangle.
midpoints
What does the "AA" stand for when we talk about "AA Similarity"?
The ratios of the lengths of the corresponding sides of two similar polygons is called:
The scale factor
Give an example of a ratio that is equal to 4:5
8:10 or 12:15 or 16:20 etc.
Solve for x:
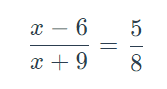

Find x:
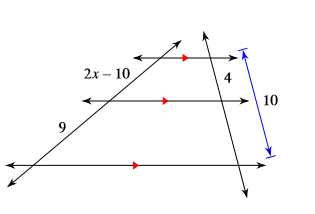
x=8
Use the Side Splitter theorem to set up a proportion:
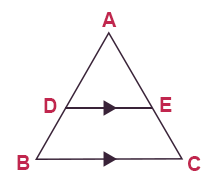
AD/DB = AE/EC
BD/DA = CE/EA
Find x. 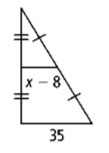
x=25.5
Are these triangles similar by AA Similarity? Explain. 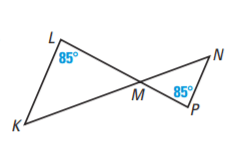
Yes since angle P is congruent to angle L and angle PMN is congruent to angle KML, then the triangles are similar by AA similarity.
What is the difference between similar polygons and congruent polygons?
Similar polygons have congruent corresponding angles but proportional sides.
Congruent polygons have congruent corresponding angles and sides.
$4.29/12oz = $.36/oz
Solve for x. 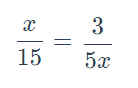

Find x.
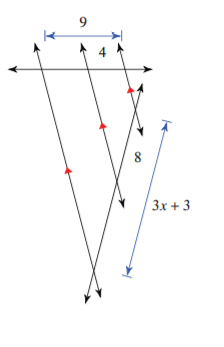
x=5
Solve for x. 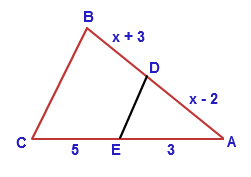
We cannot find x since we do not know if line segments DE and BC are parallel.
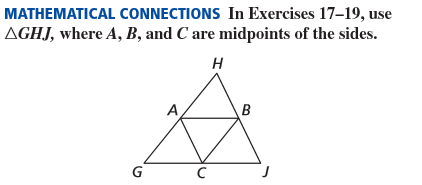
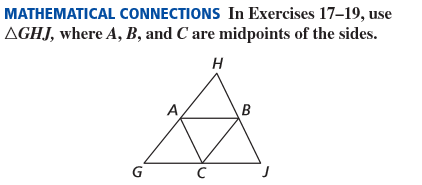 If HA = 5x-10 and AG = 4x+3, find AG.
If HA = 5x-10 and AG = 4x+3, find AG.
55
Explain why all equilateral triangles are similar by AA Similarity.
Equilateral triangles are similar by AA Similarity because two equilateral triangles will always have 3 pairs of congruent angles (60 degrees each), and since we only need two pairs of congruent angles for AA Similarity, equilateral triangles will always be similar by AA Similarity.
Find x if both polygons are similar:
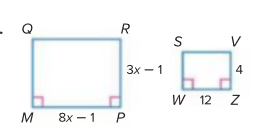
x = 2
The ratio of boys to girls in a school is 5:4. The total number of students is 810. Find the number of girls in the school.
Set up an equation:
5x+4x=810
9x=810
x=90
4(90) = 360 girls
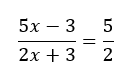
No solution.
Find x and y:
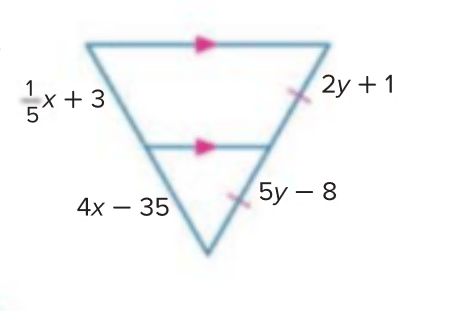
x = 10
y = 3
Find x:
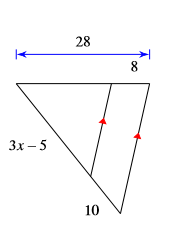
x = 10
 If AB = 4x + 2 and GJ = 6x+12, find AB.
If AB = 4x + 2 and GJ = 6x+12, find AB.
AB = 18
Are these triangles similar by AA Similarity? Explain.
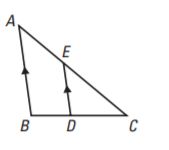
Yes since angle C is congruent to itself (reflexive POC) and angles A and CED are congruent (corresponding angles), then the triangles are similar by AA Similarity.
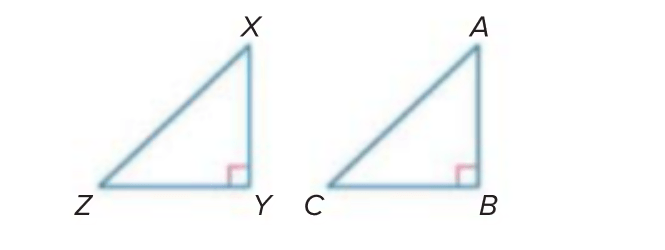
Angle Z is congruent to angle C:
1. Are these triangles similar? Why or why not?
2. If they are similar, tell me which triangle is similar to which.
Yes; two angles of XZY are congruent to two angles of ACB, so the triangles are similar by AA similarity.
Triangle XZY is similar to triangle ACB.
The exterior angles of a quadrilateral are in the ratio 2:3:4:5. Find the measure of the largest angle.
Set up an equation:
2x+3x+4x+5x=360
12x=360
x=30
5(30)=150
Solve for x. 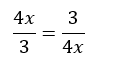
x equals plus or minus 3/4
Find x+y.
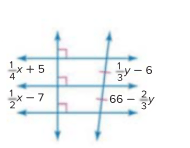
x = 48, y = 72, so x+y=120
Find the value of x3:
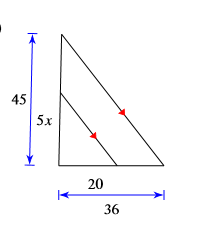
x3=125
If CA = 6x2 + 10 and HJ = 8x2 + 36
x equals plus or minus 2.
State the AA Similarity Postulate.
The AA Similarity Postulate says:
"If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar."

Scale Factor: 2
MNPQ perimeter: 34
XYZW perimeter: 17