Solve for x:
x/32 = 4/5
x = 25.6
According to SSS Similarity, what do two triangles need to have in order to be similar?
All 3 corresponding ratios must be the same.
OR
All corresponding sides must be propotional.
Solve for x given that the triangles are similar.
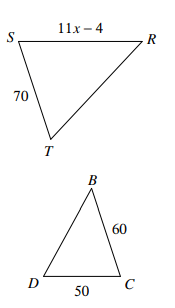
x=8
Congruent triangles are always similar triangles.
True or False
True
Dialtion: J(4, 8), K(8, 8), L(4, 2), k =0.25, centered at the origin
J'(1, 2) K'(2, 2) L'(1, 0.5)
△ABC ~△DEF
Perimeter of △ABC=25u, AB=5u, DE=6u
What is the perimeter of △DEF?
Perimeter △DEF=30u
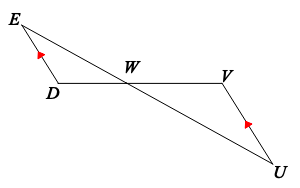
State if the triangles are similar or not and then what similarity statement makes it so.
YES, by AA Similarity
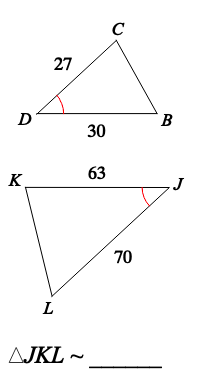
Complete the similarity statement.
Triangle DCB
Find y.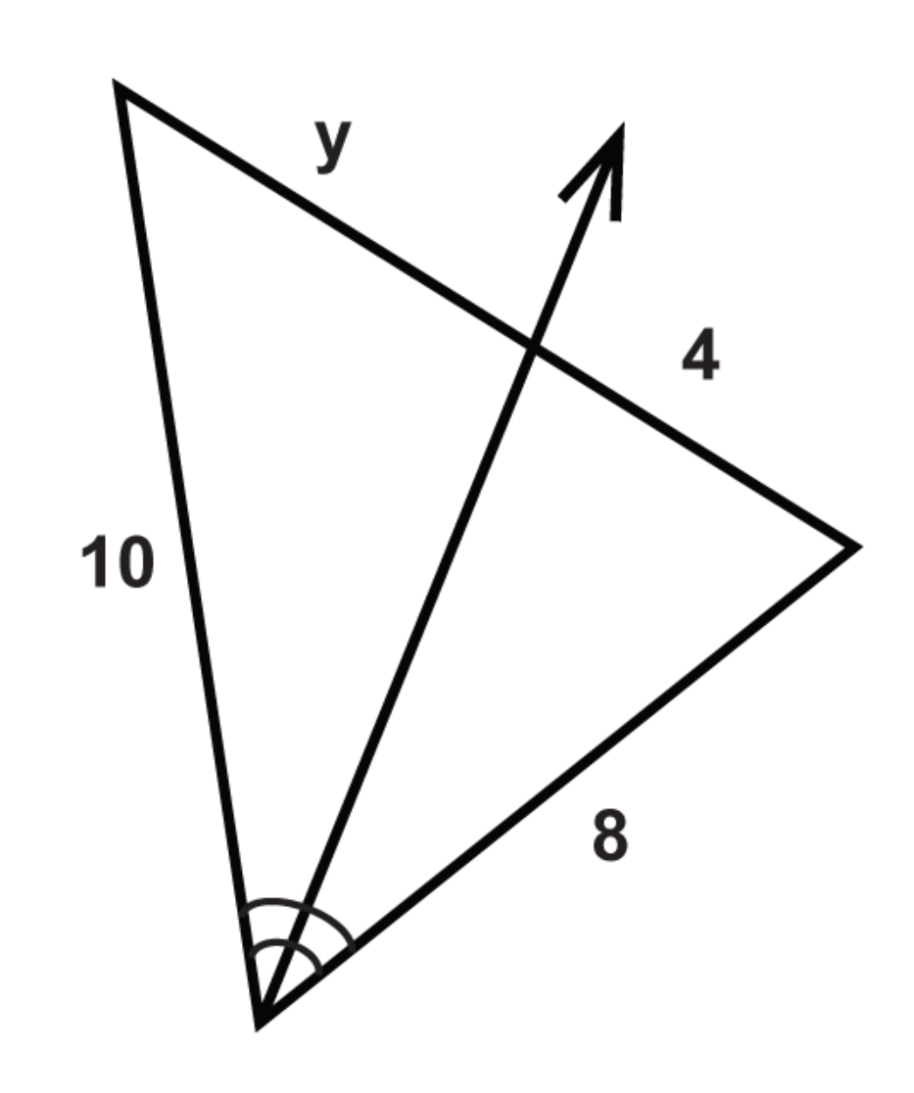
y=5
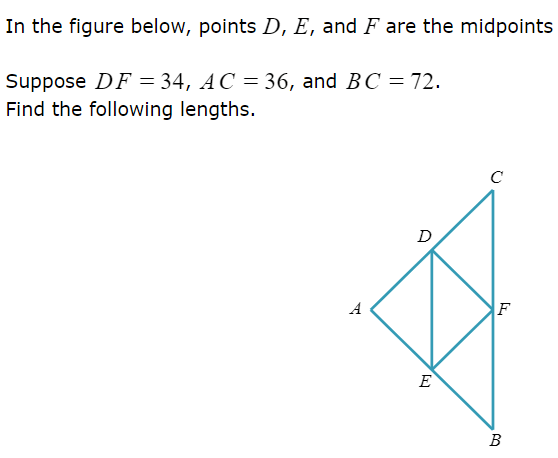
What is the measure of segment DE?
DE = 36
Dilation: 𝑇(−1, −3), 𝑈(−4, −4), 𝑉(−3, −2), 𝑘 =2, centered at T
T'(-1, -3) U'(-7, -5) V'(-5, -1)
Given two equilateral triangles with sides 16 and 20, respectively, the scale factor of the larger triangle to the smaller triangle (Hint: reduction or enlargement?)
16/20 = 4/5 = 0.2
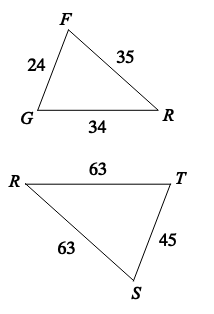
State if the triangles are similar or not and then what similarity statement makes it so.
NO, not similar
Solve for x given △VUW~△SUT.
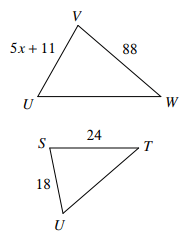
x=11
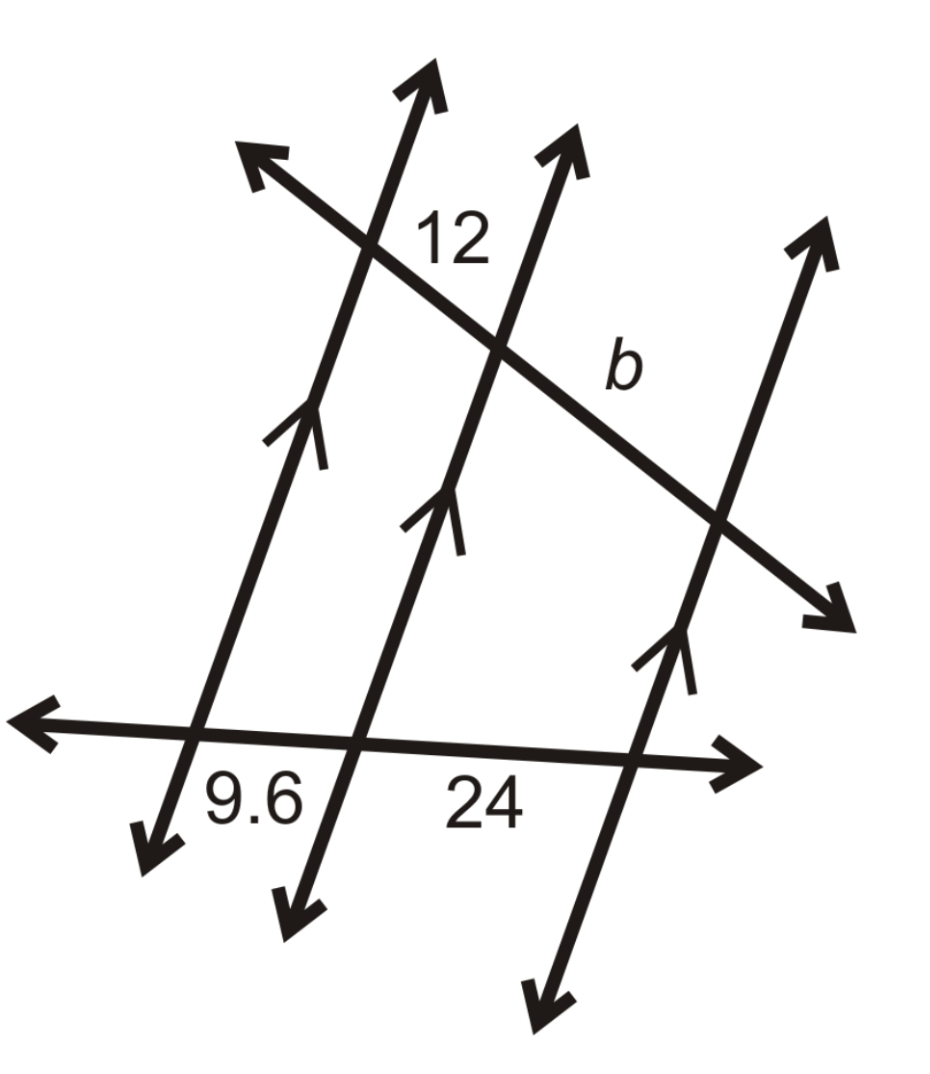 Find b.
Find b.
b=30
Our geometry class went outside to measure the height of our school’s flagpole. A student who is 5.5 feet tall stands up straight and casts a shadow that is 11 feet long. At the same time a flagpole casts a shadow that is 36 feet long. Draw a diagram to represent the situation and determine the height of the flagpole.
height = 18ft
Dialtion: 𝑄(4, 0), 𝑅(−4, −4), 𝑇(−4, 2), 𝑘 =0.5, centered at R
Q'(0, -2) R'(-4, -4) T'(-4, -1)
Solve for x.
2/3 = (x+3)/(4x)
x=3
What is it called when the lengths of two sides of one triangle are proportional to the lengths of two corresponding sides of the other triangle and the included angle is congruent
SAS Similarity
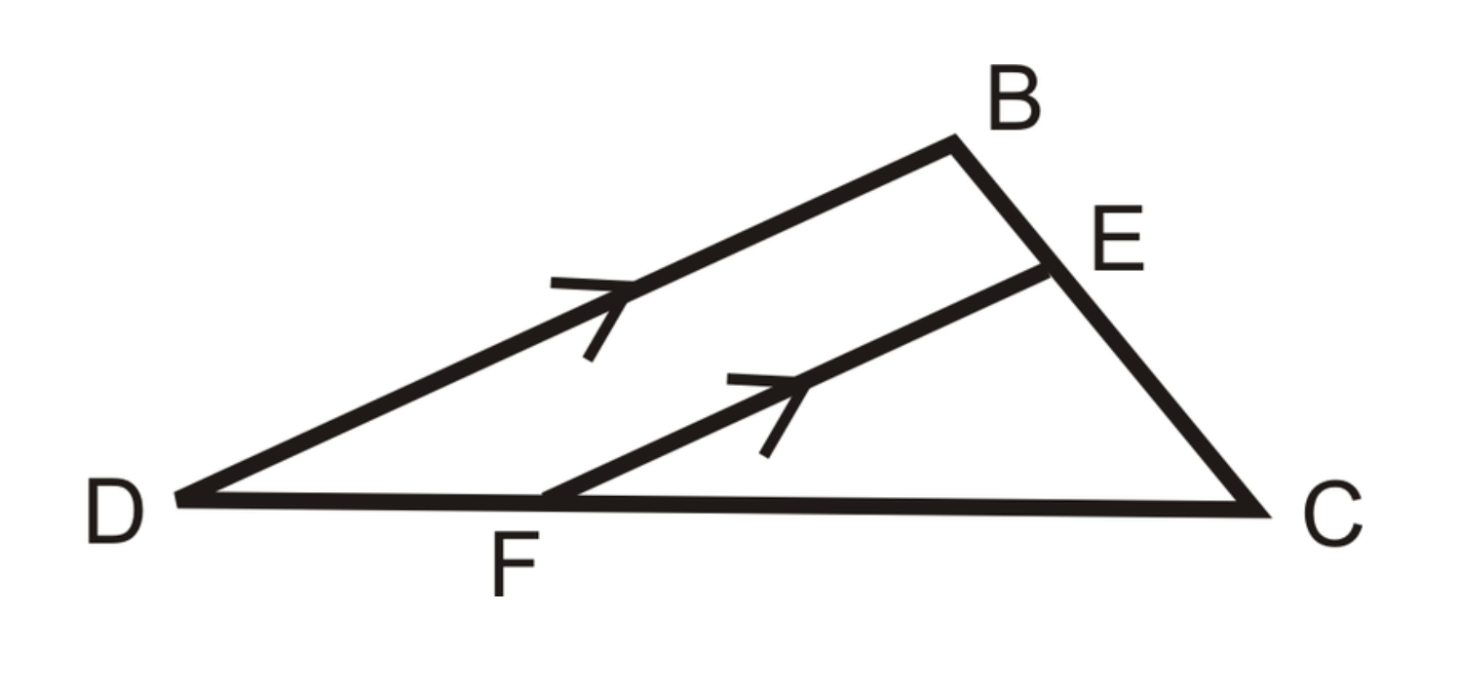
(BE)/(EC)=?/(FC)
DF
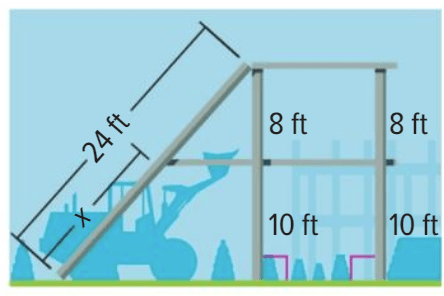
Solve for "x".
x = 13.3 ft
The diagram is an example of this type of segment.
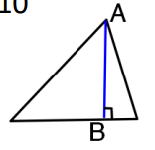
What is an Altitude?
dilation centered at the origin with a scale factor of 1.5 followed by a reflection in 𝑥 =−3 A(-3, 4) B(2, 2) C(-2, -4)
A"(-3, 7.5) B"(-9, 4.5) C"(-3, -6)
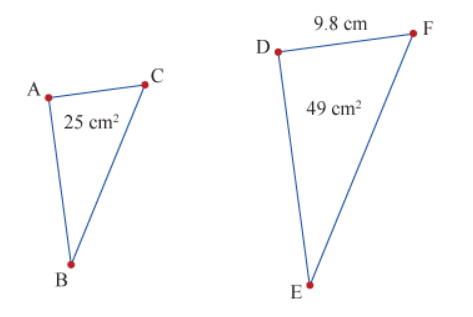
△ABC ~△DEF, find AC?
AC=7cm
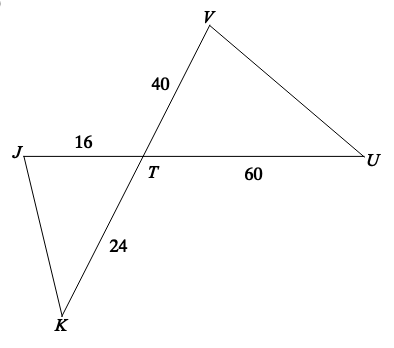
State if the triangles are similar or not and then what similarity statement makes it so.
YES, by SAS Similarity
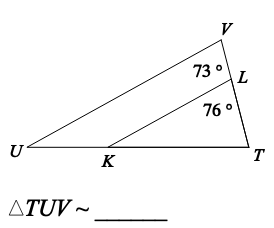
Are the triangles similar? If so, complete the similarity statement.
NOT SIMILAR
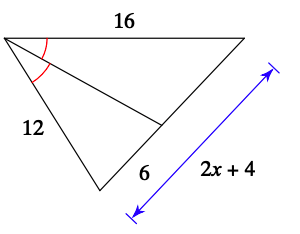
Given the angle bisector, solve for x.
x=5
Can you prove congruence? If so, write a triangle congruence statement and state which theorem you are using.
△DEF ≅ △HIG by ASA
rotation 90° counterclockwise about C followed by a dilation centered at C′ with a scale factor of 0.5 where A(-4, 5) B(2, 5) C(2, -2) D(-4, -2)
A"(-1.5, -5) B"(-1.5, -2) C"(2, -2) D"(2, -5)