Porpoise Shins
~
Stuck in the Middle
Triangle?
Area & Perimeter
Miscellanous
100
Solve for 'x'.
\frac{10}{x}=\frac{2}{7}
x=35
100
List the 3 ways to prove two triangles are similar.
AA, SAS, SSS
100
Find the length of PQ.
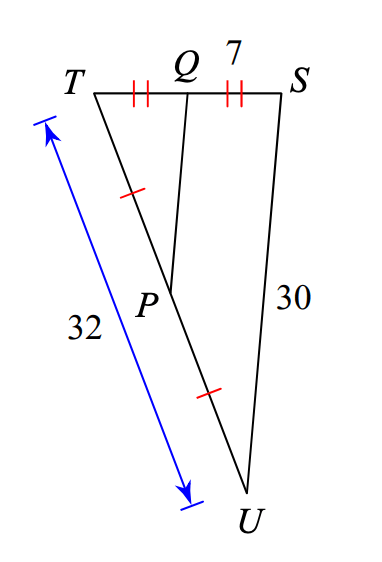
PQ = 15
100
Write an inequality to represent the possible range of lengths for the third side 'x' of a triangle with side lengths 2 and 5.
3<x<7
100
If the scale factor of two similar figures is k, then the scale factor of their areas is ________ .
k^2
100
What is the similarity ratio a:b of congruent figures?
1:1
200
Solve for 'x'.
\frac {x+1}{x+2}=\frac {5}{9}
x=1/4
200
Find the length of SB.
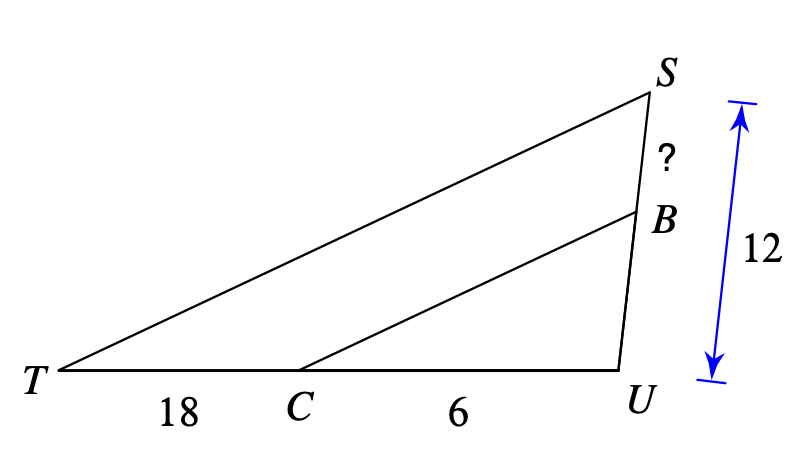
SB=9
200
Find the length of PW.
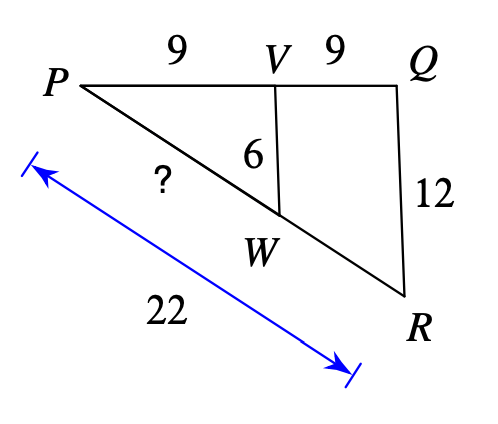
PW=11
200
Write an inequality to represent the possible values of 'x'.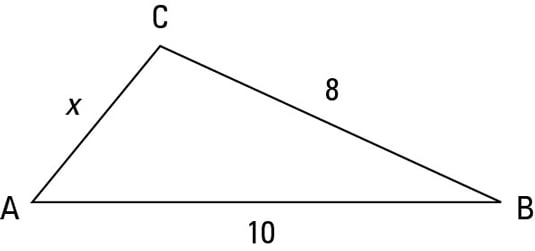 
2<x<18
200
The ratio between the side lengths of two similar polygons is 3:4. What is the ratio of the area of the figures?
9:16
200
Find the measure of the smallest angle in a triangle whose angles are in a ratio of 1:2:3.
30 degrees.
300
Solve for 'a'.
\frac{a}{25}=\frac{4}{a}
a=+-10
300
\triangleVWU~\triangleSTU.
Solve for 'x'.
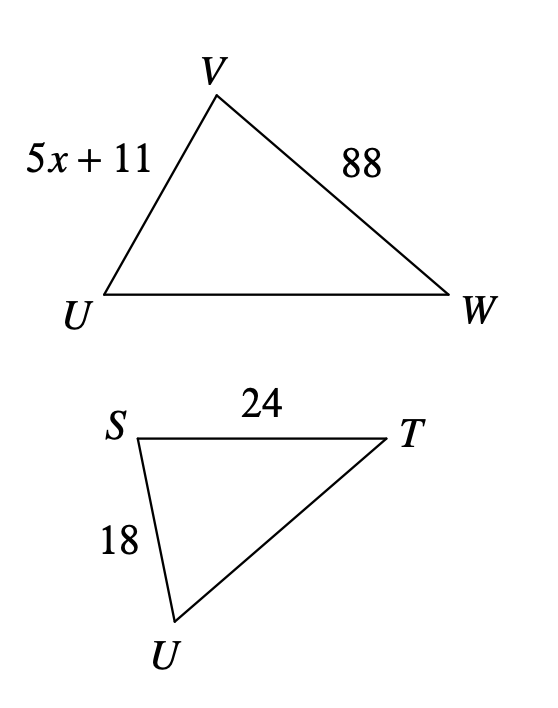
x=11
300
Find the length of ZY.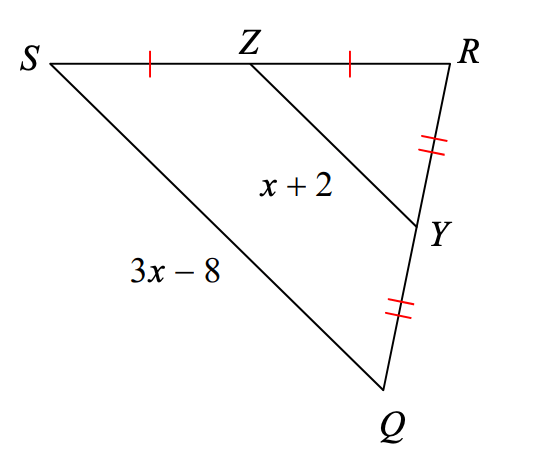 
ZY=14
300
Can a triangle be formed if the sides are in a ratio of 2:3:6? Why or why not?
No.
2+3<6
300
Two triangles are similar. The larger triangle has an area of 100 and the smaller has an area of 25. If the perimeter of the larger triangle is 20, what is the perimeter of the smaller triangle?
Perimeter of the smaller triangle is 10.
300
Find the measure of the largest angle in a triangle whose angles are in a ratio of 2:3:4.
80 degrees.
400
Solve for 'x'.
\frac{x+1}{x+2}=\frac{x-3}{x-4}
x=1
400
Find the value of 'x' and 'y'.
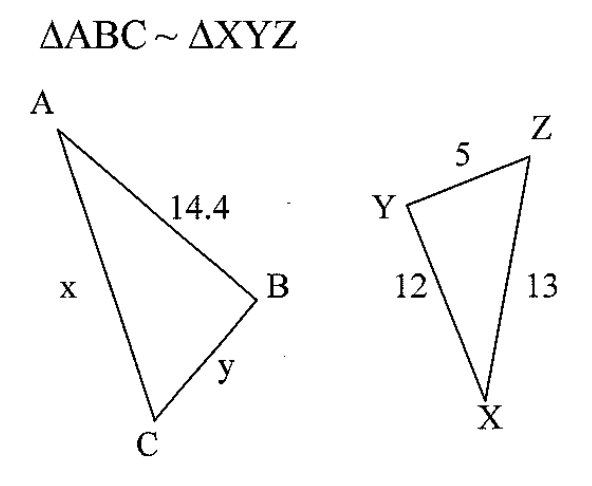
y=6, x=15.6
400
Find the length of UT.
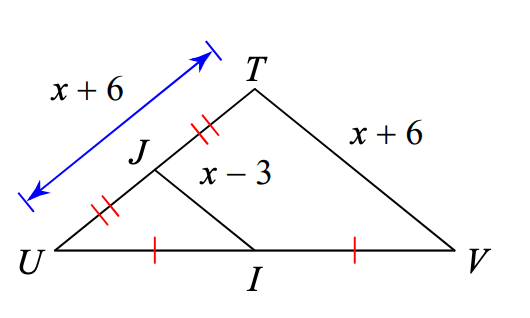
UT=18
400
Find the possible range values of 'x' that would make a triangle.
3<x<4
400
Two cubes have side lengths of 'x' and 'y', where x<y. What is the ratio of the volume of the larger cube to the volume of the smaller cube?
y^3:x^3
400
What is the probability as a percent of rolling two dice 2 times in a row and getting at least one roll that has a sum of 7.
30.6%