Substitution
Collecting like terms
Multiplying and dividing terms
Algebraic fractions
100
Substitute x=4 into this equation:
2x
8
100
Simplify:
11a + 4 − 2a + 12a
21a+4
100
Simplify:
5a × 2b
10ab
100
Simplify:
(5a)/3+(2a)/3
(7a)/3
200
Substitute x=-3 into the following:
9-x
12
200
Simplify:
11b − 3b2 + 5b2 − 2b
9b+2b2
200
Simplify:
a × a
a2
200
Simplify:
2t+(7p)/2
(4t+7p)/2
300
If a=2 and b=5, what is the value of:
ab-4+b
11
300
Write an expression for the perimeter of this shape:
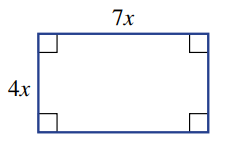
22x
300
Simplify:
3x2y × 2x × 4y
24x3y2
300
Simplify:
(4a)/3*(2b)/5
(8ab)/15
400
State whether these expressions are equivalent:
3+6y and 3(2y+1)
Equivalent
400
Write an expression for the perimeter of this shape: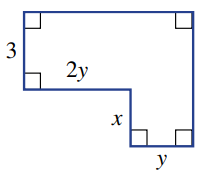
6y+2x+6
400
Simplify:
(− 15z)/ (− 20 z^2)
3/(4z)
400
Simplify:
(4a)/5/(2b)/(7a)
(14a^2)/(5b)
500
A number is substituted for x in the expression 10-2x and the result is a negative number. What does this fact tell you about the number substituted for x? (Hint: you can try different values for x to help.)
x is greater than 5 because we need the second term to be larger than 10.
500
Fill in the missing expressions to make all equations true: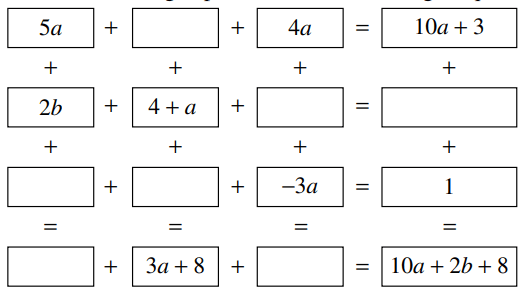
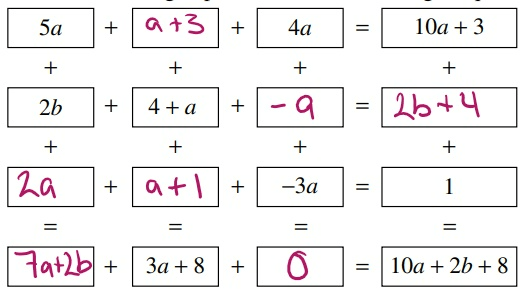
500
Simplify:
(10abc + 5cba + 5a × bc)/(4c × 10ab)
1/2
500
Helen’s family goes to dinner with Jess’ family. The bill comes to a total of $x and each family pays half.
a) Write an algebraic fraction for the amount Helen’s family pays.
b) Helen says that she will pay for one-third of her family’s bill. Write an algebraic fraction for the amount she pays.
a)
x/2
b)
x/6