Sine Law
Sides and Angles
Sides and Angles
Sine Law
(Word Problems)
(Word Problems)
Cosine Law
Sides and Angles
Sides and Angles
Cosine Law
(Word Problems)
(Word Problems)
100
Is it true that in the formula a/sinA = b/sinB = c/sinC (sine law), B is the angle opposite of side a?
No, B is the angle opposite of side b while A is the angle opposite of side a.
100
Diana and James are standing at the seashore 10 miles apart. The coastline is a straight line between them. Both can see the ship in the water. The angle between the coastline and the line between the ship and Diana is 35 degrees. The angle between the coastline and the line between the ship and James is 45 degrees. How far is the ship from James?
Find 3 angles with angle theorem: 35+ 45
180 - 80 = 100º
10/sin100º = x/sin35º
x=10sin35º/sin100º
x=5.8 m
Therefore the ship is 5.8 m from James
100
What are the conditions we should have to solve a triangle with cosine law? (require 2 answers for points) (20s)
1. Two sides and a contained angle
2. All three sides
100
Tom, Ricky, and Harry are camping in their tents. If the distance between Tom and Ricky is 153 ft, the distance between Tom and Harry is 201 ft, and the distance between Ricky and Harry is 175 ft, what is the angle between Ricky, Harry, and Tom?
1532=2012+1752-2(201)(175)cosH
23409=40401+30625-70350cosH
-47617=-70350*cosH
H=47.4º
Therefore the angle is 47.4º
200
In the pictured triangle, ∠A is 98 degrees and ∠B is 12 degrees. If side a is 84 units long, approximately how long is side b?
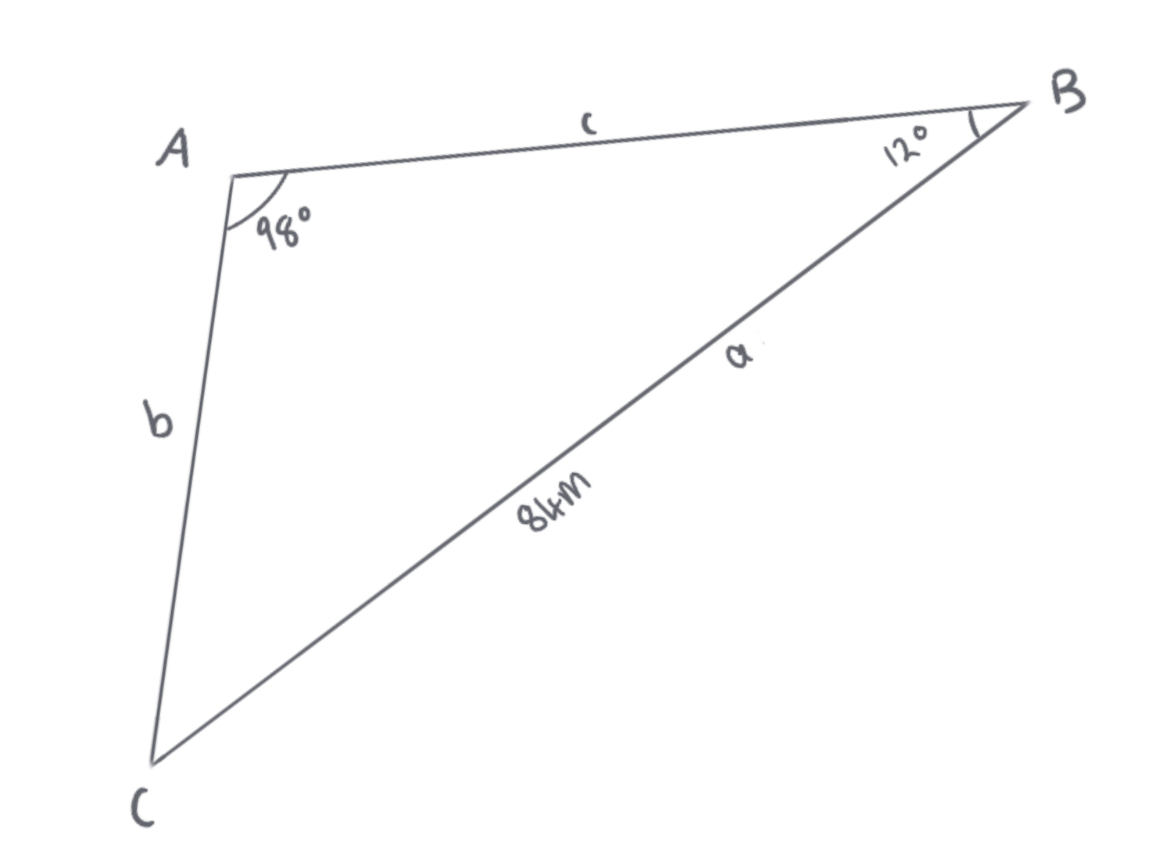
18 units
200
3 members of one direction, Harry, Niall, and Louis, decide to try out a new formation on stage. They decide to use Harry's favourite shape, a triangle. The distance from Louis to Harry is 8ft, and the distance from Harry to Niall is 7 ft. the angle formed at Niall is 70º. What is the angle formed at Louis?
sinL/7=sin70º/8
L = sin-1(7(sin70º)/8)
L = 55.3º
Therefore Louis forms a 55.3º angle.
200
Solve for B to the nearest tenth of a degree
192=82+142-2(8)(14)cosX
361= 64+196-224cosX
-101=-224cosX
cosX=101/224
X=cos-1(101/224)
X=63.2º
200
The backyard of a house is in the shape of a triangle with two sides measuring 18.3 m and 12.1 m and the angle between these two sides is 32.7 degrees. Find the length of the third side of the triangle.
The missing side length is 10.4 m.
300
Find the obtuse angle (to the nearest tenth of a degree) such that:
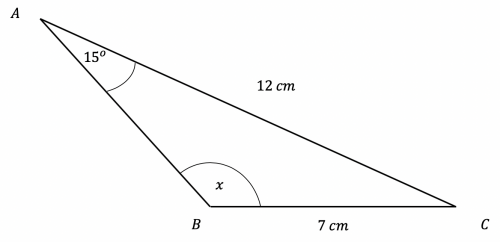
sinX/12 = sin15º/7
X= sin-1(12(sin15º)/7)
X = 26.3º
Obtuse angle: 180º-X
180º-26.3º=153.7º
X = 153.7º
300
The trumpet, clarinet, and flute sections formed a triangle during marching band practice. The clarinet line made a 34° angle with the flute line. The flute line made a 107° angle with the trumpet line. If the flute line was 27 feet long, find the length of the clarinet line.
x/sin107º=27/sin39º
x=41.0 ft
Therefore the length of the clarinet line is 41 ft.
300
Solve for the unknown angle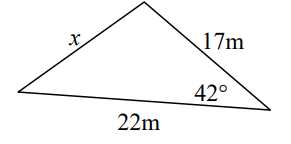
X = 14.7m
300
To approximate the length of a lake, a surveyor starts at one end of the lake and walks 245 yards. He then turns 110º and walks 270 yards until he arrives at the other end of the lake. Approximately how long is the lake? (Hint: He walked the two sides of a triangle.)
x2=2702+2452-2(270)(245)cos70º
x2=132925-132300cos70º
x=296.1
Therefore the lake is 296.1 yards long.
400
Triangle PQR has ∠P = 63.5° and ∠Q = 51.2° and r = 6.3 cm. What are the side lengths of p and q?
p = 6.21cm
q = 5.40 cm
400
A cottage under construction is to be 12.6 m wide. The two sides of the roof are to be supported by rafters that meet at an angle of 50 degrees. How long should the rafters be if they are the same length?
∠A + ∠C + 50 degrees = 180 degrees
2x + 50º = 180º
2x = 180 - 50
2x = 130
x = 65º
a/sinA = b/sinB
a/sin65º = 12.6/sin50º
A = 12.6(sin65)/ sin50
A =14.9 m
Therefore the rafters should be 14.9 m in length.
400
62=3.52+42-2(3.5)(4)cosθ
36=12.25+16-28cosθ
7.75=-28cosθ
<θ=106º
106-90=16º (how far from the vertical)
A:16º
400
A bicycle race follows a triangular course. The 3 legs of the race are, in order, 2.3 km, 5.9 km and 6.2 km. Find the angle between the starting leg and the finishing leg, to the nearest degree.
the angle is 72 degrees
500
Solve the missing angles and side lengths of ∆ABC where side A is 8cm, side b is 4cm, and angle C is 53 degrees. Round to one decimal point
Side lenght c = 6.4cm
Angle B = 29.9 degrees
Angle A - 180 - 29.9 - 53 = 97.1 degrees
500
A wall that is 1.4 m long has started to lean and now makes an angle of 80o with the ground. A 2 m board is jammed between the top of the wall and the ground to prop up the wall. What angle does the board make with the ground?
2/sin80º = 1.4/sinS (any variable is fine)
S = 1.4sin80º / 2
S = sin-1 (1.4sin80º / 2)
S = 44º
Therefore the board makes a 44º angle with the ground.
500
Solve the for the missing angle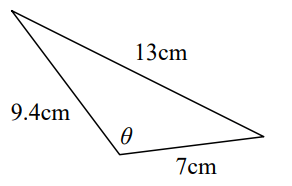
Θ = 103.9 degrees
500
A farmer has a field in the shape of a triangle. The farmer has asked the manufacturing class at your school to build a metal fence for his farm. From point A to point B, it is 435 m. From point A to point C it is 656 m. The angle at point A is 49 degrees. Calculate how much fencing he would need to enclose his entire field.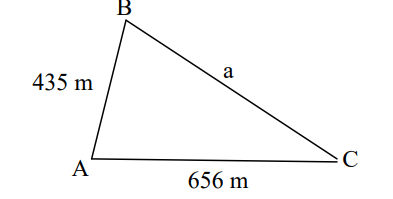 
The amount of fencing required is 495m