Writing Equations
Slopes And Graphs
Converting Forms
Real-World Problems
100
A streaming platform charges a base fee of $8 per month plus $0.50 per video downloaded.
Write an equation for the total cost (C) after downloading (v) videos.
C=8+0.5v
100
What is the slope and y-intercept of y=2x+1
slope= 2
y-int. = 1
100
Write 2x−y=10 in slope-intercept form.
y=2x-10
100
Movie tickets cost $14 (adult), $8 (child) with a budget of $280. Write the equation if cost equals $280, (a) adults go, and (c) children go.
280=14a+8c
200
A gym charges $20 to join and $5 per class attended.
Write an equation where (X) classes are attended.
C=20+5x
200
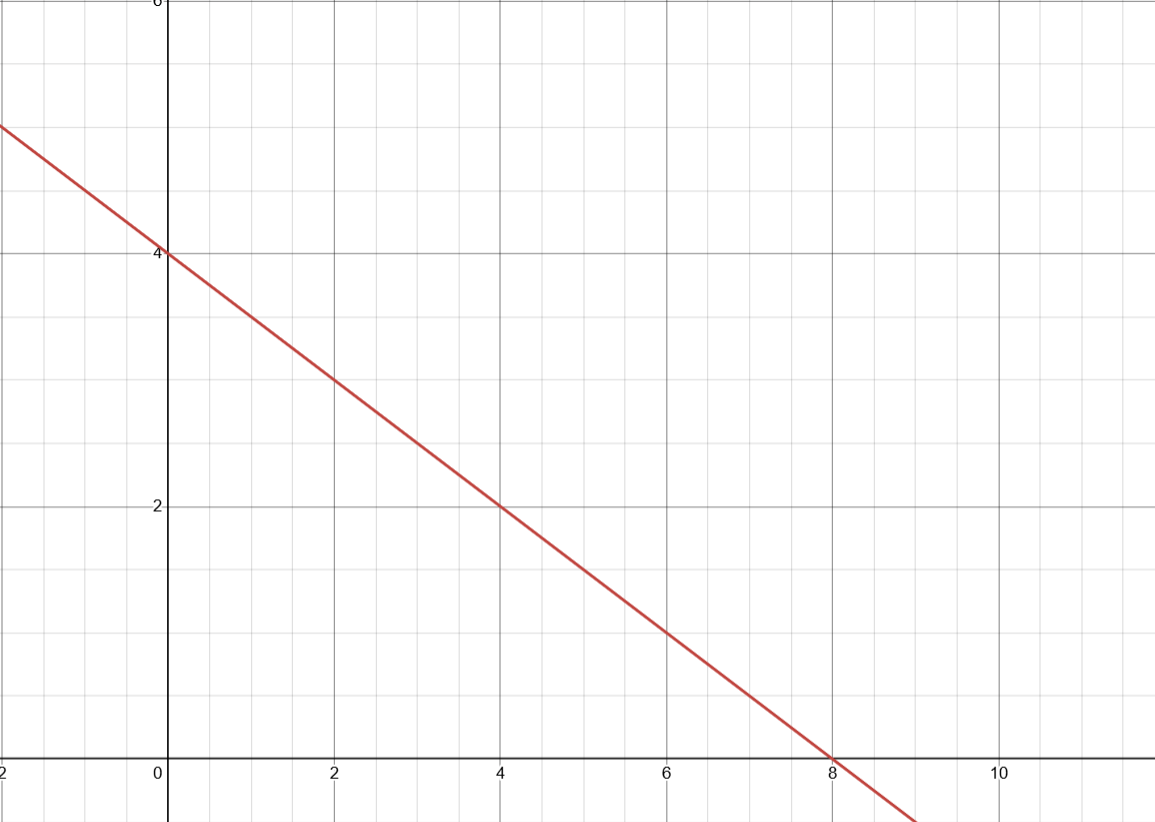
Graph y=
-1/2x +4
200
Convert 3x+2y=8 to slope-intercept form.
y=
-3/2x+4
200
A gym membership charges $25 base fee and a $3 charge per visit. Write the equation if (v) visits are made.
C=25+3v
300
A food truck charges $4 for a taco and $1.50 per drink.
Write an equation where C= Cost and (T) tacos, (d) drinks are bought.
C= 4T+1.50d
300
What is the slope and y-intercept for the line 5x-y=15
slope= 5
y-intercept= -15
300
Rewrite the equation 6x−2y=10 in slope-intercept form.
y=3x-5
300
Concert tickets cost $30 (adult), $20 (student), budget $500.
1.Write equation when budget is $500.
2. If 15 adults (a) go and 12 students (s) go, what is the cost?
1. 500=30a+20s
2. 30(15)+20(12)=690
400
A video rental service charges $12/month and $2 per rental.
Write an equation to model the cost (C) if (r) movies are rented.
C=12+2r
400
Find the slope of the line through the points (2,4) and (6,8)
slope= 1
400
A line passes through the points (–2, 5) and (4, –1).
Write the equation of the line in slope-intercept form.
Slope = -1
400
A bakery sells cupcakes for $3 each and cookies for $2 each. The total amount earned in one day was $90.
If they sold 10 cupcakes, how many cookies did they sell?
3(10)+2x=90
90-30= 60
60/2= 30 cupcakes
500
A bowling alley charges a $10 lane fee plus $3 per game per person.
1. write an equation if (p) persons are playing.
2. Solve the equation of p=15
1. 10+3p
2. 10+3(15)= $55
500
A line has a slope of -3 passing through (0,7). Write equation.
y= -3x+7
500
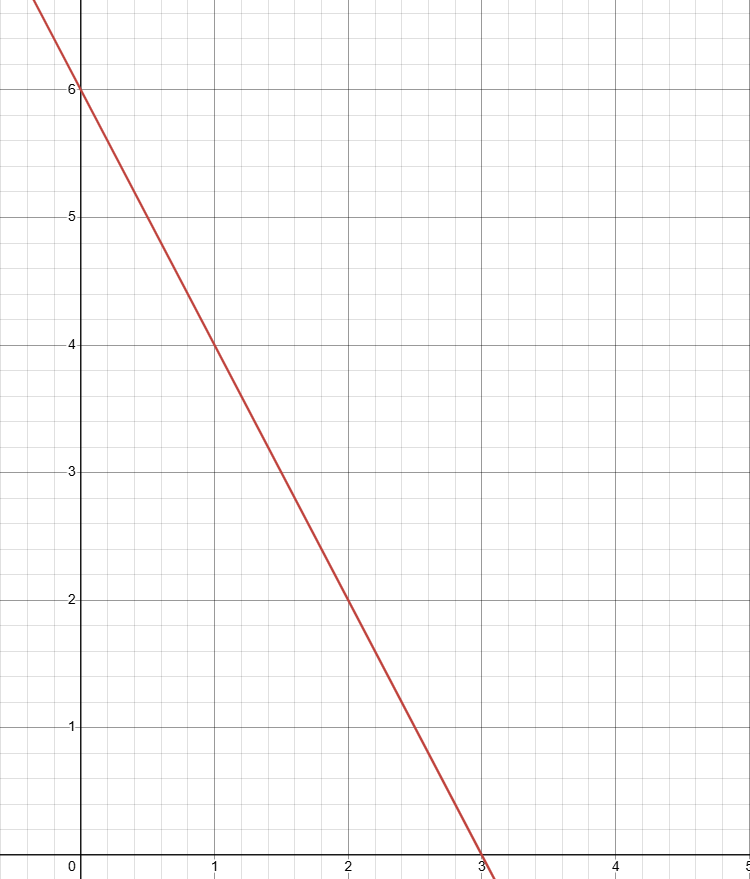
Graph 4x+2y=12
State Slope and Y-Int.
500
A car rental company charges $40 per day and $0.20 per mile driven.
A customer has $160 to spend.
Write an equation and determine how many miles the customer can drive if they rent the car for 2 days.
160=40(2)+0.20m
160=80+0.20m
subtract 80 from both sides
80=0.20m
divide both sides by 0.20 and m=400