Linear Equations
Intercepts
Zeros
ROC
Slope
Slope-Intercept Form
100
Give ONE example of something that would make an equation nonlinear
xy
an exponent
1/x
100
The x-intercept is where y = _____
0
100
What is a zero?
An x-intercept
100
Find the rate of change:
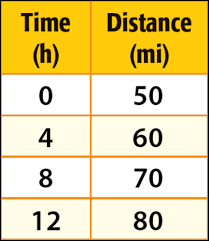
2.5 miles per hour
100
What is the slope formula?
m = y2 - y1/x2 - x1
100
Write an equation in slope intercept form with a y-intercept of -8 and a slope of 10
y = 10x - 8
200
Write in slope-intercept form:
3x + y = 12
y = 12 - 3x
or
y = -3x + 12
200
Identify the x and y-intercepts:
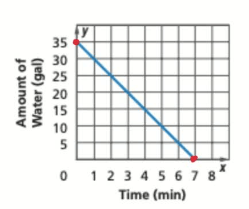
y = 35
x = 7
200
What equation would be the same as f(x) = 2x + 1
y = 2x + 1
200
Find the rate of change:
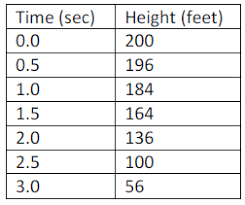
-8 feet per second
200
Find the slope:
m = -3/4
200
Write the equation 3x + 4y = -16 in slope intercept form and state the slope and y-intercept
y = -4 - 3/4x
slope: -3/4
y-int: -4
300
Write in standard form:
y = 2x + 9
2x - y = -9
300
Describe what the x-intercept of the graph means.
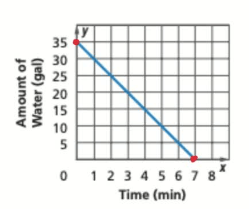
In 7 minutes there will be 0 gallons of water
300
Find the zero(s):
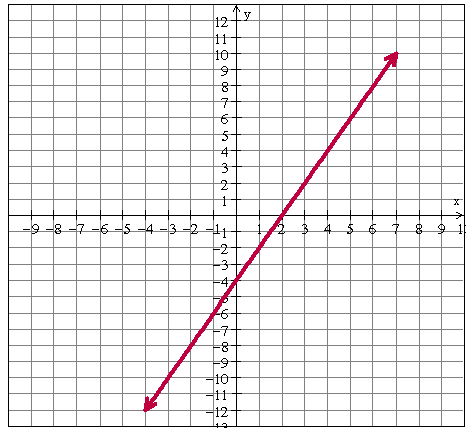
x = 2
300
Find the rate of change from 2 to 4 hours:
-15 mph
300
Find the slope:
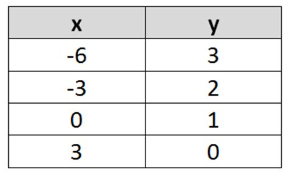
m = -1/3
300
Write the equation of the line:
y = 2x - 1
400
Write in slope-intercept form:
1/3x + 2y = 6
y = 3 - 1/6x
400
Identify the x and y-intercepts from the table:
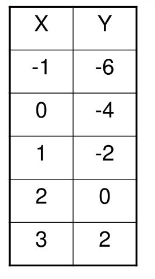
x = 2
y = -4
400
Find the zero of the function f(x) = 18 + 8x
-9/4
400
Round your answer to the nearest tenth:
4.3 cm/year
400
Find the slope between the two points:
(1, 5) (3, 8)
3/2
400
At 5 am the temperature was 58o and then in climbed steadily throughout the morning at a rate of 2o an hour. Give and equation, T, of the temperature after h hours.
T = 58 + 2h
500
Write in standard form:
1/2y = 8 + 1/6x
2x - 6y = -96
500
Find the intercepts:
7x - 9y = -126
x = -18
y = 14
500
The function y = -15 + 3x represents the outside temperature, in degrees Fahrenheit, in a small Alaskan town where x represents the number of hours after midnight. The function is accurate for x-values representing midnight through 4 pm. Find the zero of the function.
5 degrees
500
Sally is draining her pool to get ready for winter. She had 1534 cubic feet of water in the pool at 8 am this morning and it was down to 841 cubic feet by the time she got home from work at 5 pm. Calculate the rate of change of the water per hour during the day.
77 cubic ft/hour
500
Solve for "r":
(-4, 8), (r, 12), m = 4/3
r = -1
500
Paul joins a gym that has an initial membership fee and a monthly cost. He pays a total of $295 after three months and $495 after eight months. Find the initial membership fee and the monthly cost and use them to write an equation for the total cost as a function of the number of months
initial fee: 175
monthly cost: 40
y = 40m + 175