What formula do we use to calculate the average rate of change?
What is the name of the graph of a quadratic function?
Parabola
What is the Vertex of this graph?
f(x)= -(x-5)²-8
(5,-8)
What is the solution of 3(2x+4)−5=2(x+6)+7
x=3
What key feature of a parabola will give you the maximum height of an object?
Hint: Be specific, Which coordinate x or y?
THE Y-COORDINATE OF THE VERTEX
Solve the equation for x.
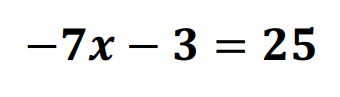
x=-4
What is the name of the line that cuts the graph of a quadratic in half?
AXIS OF SYMMETRY
What is the y-intercept of the parabola with the following equation?
y=x2 -6x +8
(0,8)
What value makes this equation true, 5(y−2)+4(y+3)=3(2y+1)+9
x= 10/3
What key feature of a parabola will give you the initial height of an object?
THE Y-INTERCEPT
Identify the slope and y-intercept given the equation below.
y = -x + 7
slope: -1
y-intercept: 7
What is the name of the maximum or minimum of a quadratic function?
Vertex
What is the vertex of the parabola?
y= -0.5(x+4)2 +6
(-4,6)
what is the solution of 7(x+1)−2(3x−4)=5(x−2)+3
x=11/2
A ball is thrown into the air. It's height h, in feet after t seconds is given by the function h(t)=−16t2+48t+4
What was the 𝐢𝐧𝐢𝐭𝐢𝐚𝐥 𝐡𝐞𝐢𝐠𝐡𝐭 of the ball when it was thrown?
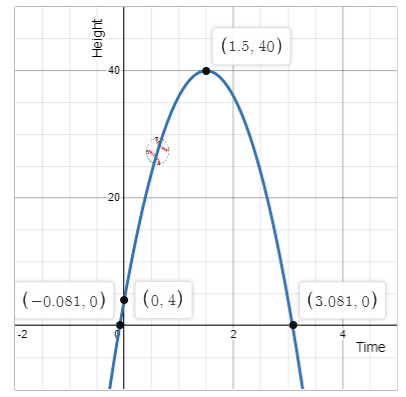
4 feet
Evaluate the function below for f(2).
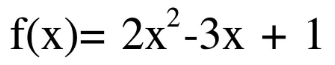
f(2)=3
What are the other names for x-intercepts of a Parabola?
Hint: There are three other names we can use.
Solutions, Roots and Zeros
What are the x-intercepts of the quadratic function with the following equation?
f(x)=-1/2(x-6)(x+8)
(6,0) and (-8,0)
whats the solution
5(z+2)=3(z+6)−4
z=2
The graph shows the height h in feet of a small rocket t seconds after it is launched. The path of the rocket is given by the equation:
h(t) =−16t2+128t
𝐇𝐨𝐰 𝐥𝐨𝐧𝐠 𝐢𝐬 𝐭𝐡𝐞 𝐫𝐨𝐜𝐤𝐞𝐭 𝐢𝐧 𝐭𝐡𝐞 𝐚𝐢𝐫?
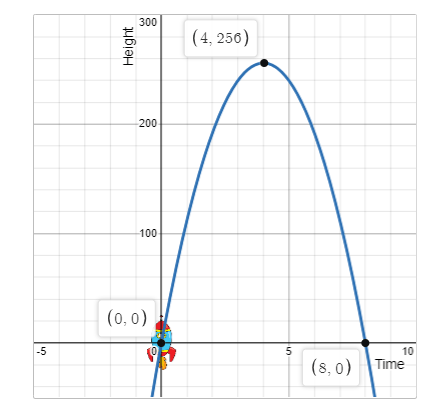
8 seconds
Solve the inequality for x.
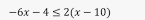
2<=x
x>=2
What is the set of all possible x-values and y-vales called?
Hint: There are two vocabulary words you need for the answer.
What is the axis of symmetry for the parabola with the following equation?
h(x)=3x2 -24x+45
2.5x+7.5=1.5(x+10)
x=7.5
What was the height of the football after 4 seconds?
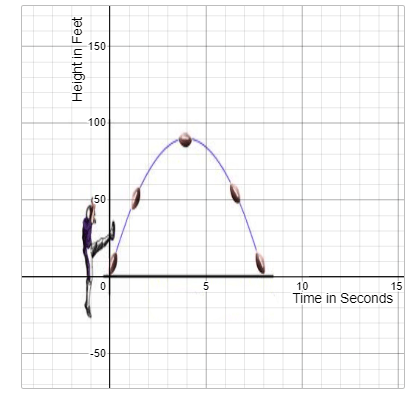
90 feet