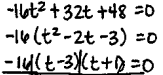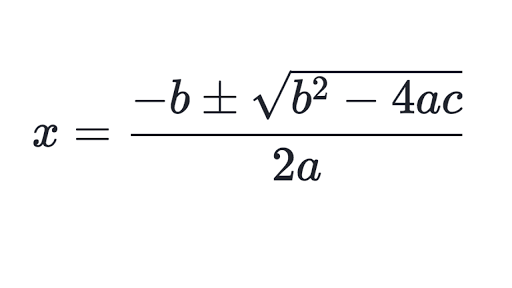Solve this quadratics by factoring to find the x-intercepts.
x2 + 2x = 3
x2 + 2x - 3 = 0
(x-1)(x+3) = 0
x = 1 or x = -3
Solve
x^2-2x-4 = 0
by completing the square.
x^2-2x = 4
x^2-2x+1 = 5
(x-1)^2 = 5
x-1 = +-sqrt(5)
x = 1+-sqrt(5)
When solving using the quadratic formula, what is the first 2 things you should do?
1st - make sure it is in standard form
(ax2 + bx + c = 0
2nd - Write down the values of;
a =
b =
c =
Solve this equation by taking square roots.
x2 + 1 = 37
x2 = 36
x= 6, -6
How is standard form written for a quadratic equation?
y = ax2 + bx + c
or
ax2 + bx + c = 0
Find the axis of symmetry.
y = 2x^2-8x+1
x = -b/(2a)
x = 8/4 = 2
Find x if area of the rectangle is 21.
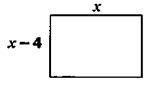
x(x-4) = 21
x^2-4x = 21
x^2-4x-21 = 0
(x-7)(x+3) = 0
x = 7 or -3
x = 7
Solve this quadratics by factoring to find the x-intercepts.
X2 + 16 = 10x
x2 - 10x + 16 =0
(x-2)(x-8)
x = 2 or x = 8
Solve x2 − 6x − 3 = 0 by completing the square.
x2−6x=3
x2−6x+(−3)2=3+9
(x−3)2=12
x−3=±√12
x = 3±2√3
x=6.46 and -.46
Solve using the quadratic formula for this equation;
2m2 + 2m − 12 = 0
a = 2, b = 2, and c = -12
x = -(2) ±√ (2)2 - 4(2)(-12) / 2(2)
x = 2 and -3
Solve this equation by taking square roots.
x2 - 10 = 54
x2 = 64
x = 8 , -8
How is vertex form written for a Quadratic Equation?
y = a(x-h)2 + k
or
a(x-h)2 + k = 0
Find the vertex.
y = 3(x+6)^2-7
(-6,-7)
The product of two consecutive positive integers is 30. Find the two integers
x(x+1) = 30
x^2+x-30 = 0
(x+6)(x-5) = 0
x = -6,5
x = 5
5 and 6
Solve for x by factoring
8x^2 = 10x
8x^2-10x = 0
2x(4x-5) = 0
x = 0, 5/4
Solve x2 - 6x + 7 = 0
x2 - 6x = -7
x2 -6x + (3)2 = -7 + 9
x2 -6x + 9 = 2
(x-3)2 = 2
x -3 = ± √2
x = 3± √2
x = 4.42 and 1.59
Solve x2 + 4x - 21 = 0 by using quadratic formula.
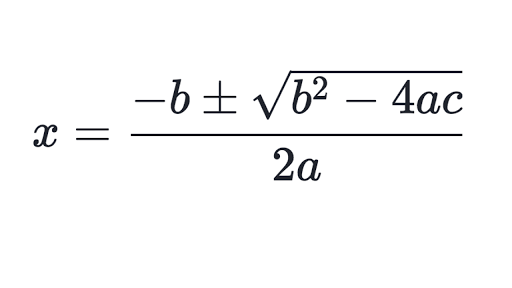
a = 1, b = 4, and c = -21
x = 3 or -7
Solve this equation by taking square roots.
5x^2-15=45
5x^2=60
x^2=12
x = ±2sqrt(3)
What is the formula to find the axis of symmetry of a standard form.
x =- b/(2a)
Find the vertex.
y = 2x^2+4x
x = -b/(2a)
x = -4/4 = -1
y = 2(-1)^2+4(-1)
y = -6
vertex = (-1,-6)
The length of a rectangle is 1 meter less than its width. The area of the rectangle is 42 square meters. Find the DIMENSIONS of the rectangle.
x(x-1) = 42
x^2-x-42 = 0
(x+7)(x-6) = 0
x = 6
6m, 7m
Solve this quadratics by factoring to find the x-intercepts.
18x2 - 3x = 6
18x2 - 3x -6 = 0
= 3(6x2 - x - 2) = 0
= 3(3x -2)(2x +1)= 0
= 3x -2 = 0 2x + 1 = 0
x = 2/3 or x -1/2
Solve
x^2+71 = 18x-19
by completing the square.
x^2-18x = -80
x^2-18x+81 = 1
(x-9)^2 = 1
x-9 = +-1
x-9 = 1 or x-9 = -1
x = 10, -8
Solve x2 - 8x + 14 = 0 using the quadratic formula.
a = 1, b = -8, and c = 14
x = -(-8) ±√ (-8)2 - 4(1)(14) / 2(1)
= 8 ±√ 8 / 2 = 8 ±2√ 2 / 2
=4 ±√ 2
= 5.41 and 2.59
Solve this equation by taking square roots.
(x-4)2 - 16 = 0
(x-4)2 = 16
x- 4 =± 4
x = 0 or 8
What transformations are being performed for the quadratic equation below?
y = 1/2(x-5)^2+4
Compression by half, right 5, up 4
Find the domain and range
y = x^2-4x-5
Domain
(-infty, infty)
Range
[-9, infty)
A toy rocket is launched from a platform that is 48 feet high. The rocket's height above the ground is modeled
h = -16t^2+32t+48
Find the maximum height reached by the rocket.
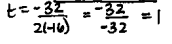

Solve the following by factoring.
81x^2-25 = 0
a = 9x, b = 5
(9x+5)(9x-5) = 0
x = ± 5/9
Solve
2x^2-16x+22 = 0
by completing the square.
x^2-8x+11 = 0
x^2-8x = -11
x^2-8x+16 = 5
(x-4)^2 = 5
x-4 = +-sqrt(5)
x = 4+-sqrt(5)
Solve 2x2 = 7x + 6 by using quadratic formula.
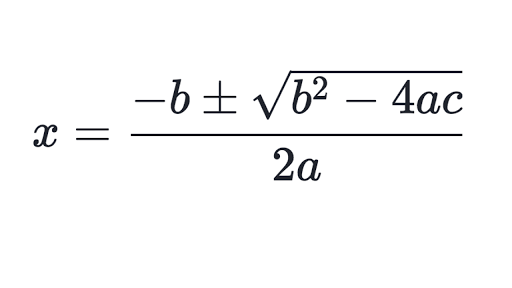
a = 2, b = -7, and c = -6
x = -(-7) ±√(-7)2 -4(2)(-6) / 2(2)
x = (7 ±√ 97) / 4
x =4.21 and -.71
Solve this equation by taking square roots.
(x+7)2 - 11 = 0
(x+7)2 = 11
x + 7 = ±√11
x = -3.68 and -10.32
Convert the following to factored form
(x+4)^2-1
(x+4)(x+4)-1
x^2+8x+16-1
x^2+8x+15
(x+5)(x+3)
A toy rocket is launched from a platform that is 48 feet high. The rocket's height above the ground is modeled
h = -16t^2+32t+48
Find the maximum height reached by the rocket.