When solving systems of equations algebraically which statement results in Infinitely many solutions?
a. x=0
b. 5=3
c. 2=2
d. -6 =6
c. 2=2
Simplify
(2x - 5)^2
4x^2 -20x +25
What is the solution?
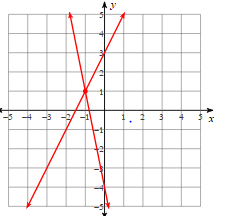
(-1,1)
Solve the systems of equations using substitution:
-x + 4 = y
2y = -2x + 8
Infinitely many
Solve.
14x + 2y = 26
-14x - 6y = -50
(1, 6)
Free Square
Free Point!
−5n − 8(1 + 7n) = −8
n= 0
How many solutions are there?
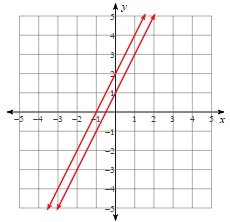
No Solutions
Solve the systems of equations using substitution:
-5x - 5y = 10
y = -3x
(1, -3)
Solve
a. -3x - 24y = -66
b. 3x + 4y = -14
(-10, 4)
When solving systems of equations algebraically which statement results in one solution? Choose all that applies.
a. x=12
b. x=0
c. -5=x
d. 2=0
e. 6=6
a. x=12
b. x=0
c. -5=x
|4x+3|=11
x = 2 AND x = -14/4 = -3.5
Solve the system by Graphing
y = -3/4x + 4
y = 1/2x - 1
(4, 1)
Solve the systems of equations using substitution:
8y = 4x
3x -6y = 9
no solution
Solve
15x - 6y = 36
8x - 6y = 22
(2,-1)
When solving systems of equations algebraically which statement results in no solutions?
a. 0=0
b. 3=0
c. 7=x
d. 4=-4
e. x=0
b. 3=0
d. 4=-4
8p^4 (−9p^4 −7p + 3)
-72p^8 - 56p^5 + 24p^4
Free Square!
You get One Point
Solve the systems of equations using substitution:
-8x - 5y = -24
y -10 = x
(-2, 8)
Solve the systems of equations using Elimination:
3x + 2y = 4
x + y = 8
(-4, 12)
Julio's school is selling tickets to the annual dance competition. On the first day of ticket sales the school sold 2 senior citizen tickets and 13 child tickets for a total of $172. The school took in$220 on the second day by selling 8 senior citizen tickets and 13 child tickets. What is the price each of one senior citizen ticket and one child ticket?
;)
On Word doc
Product : (x-5)(x+3)
Sum: x^2 -2x -15
On word doc!
A. 4 months
B. $140 Beginners Plan and Veteran about $160
Solve the systems of equations using substitution:
y = -7 + 8x
16x - 2y = 14
Infinitely Many Solutions
2x+8y=6
-5x-20y=-15
Infinite Solutions