Overview
Solving Systems: Graphing
Solving Systems: Substitution Method
100
1)
What shape will every linear equation create when graphed in the coordinate plane?
Line
100
6)
The solution to a system of linear equations is the point at which the two lines _______________.
intersect
100
11)
The first step of solving using the substitution method has you _____________ one of the variables from the other equation so that there is only _________ type of variable in the equation.
substitute (replace), one
200
2)
At least how many equations will be in a system of linear equations?
At least 2 equations will be in a system of linear equations.
200
7)
What is the solution to the system of linear equations?
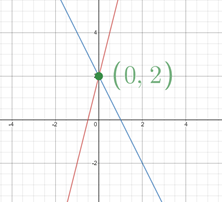
(0,2)
200
12)
What is the solution (x,y) to the system of linear equations?
y = 2x - 4
y = 4
(4, 4)
300
3)
The ___________________ to a system of linear equations is the ____________ where the equations have values for x and y that make both equations true.
solution, point (ordered pair)
300
8)
What is the solution to the system of linear equations?
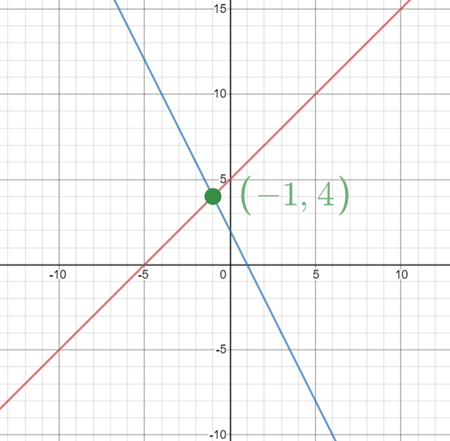
(-1,4)
300
13)
What is the solution to the system of linear equations?
y= -3x - 4
y = x
(0, 1)
400
4)
How many solutions can a system of linear equations have?
0, 1 or all
400
9)
What is the solution to the system of linear equations?
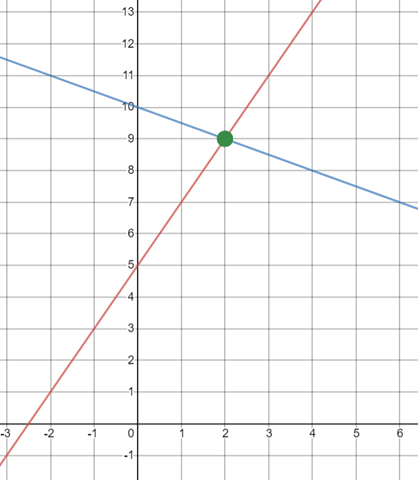
(2,9)
400
14)
What is the solution to the system of linear equations?
y= -3x + 12
y= 2x - 3
(3, 3)
500
5)
Fill in the blanks:
The solution will be the point
( , ) where the two lines
________________
(x,y), intersect
500
10)
What is the solution to the system of linear equations?
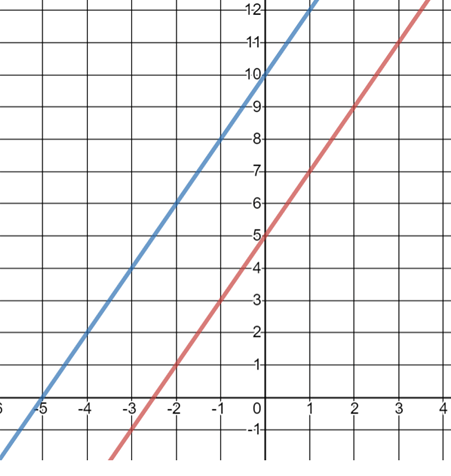
No solutions
500
15)
What is the solution to the system of linear equations?
y=2x+4
y=-3x-11
(-3,-2)