How many ways are there to get a four of a kind in a 5-card poker hand made from a standard 52-card deck? (Recall there are 4 suits and each suit has one card of 13 ranks.)
((13),(1))((12),(1))((4),(1)) = 13 xx 12 xx 4 = 624
In 1489, German mathematician Johannes Widmann published Mercantile Arithmetic, the first printed book where these two symbols were used to denote either surplus or deficit.
+ and -
Suppose 150 M&M's are distributed as follows among three jars: One jar has 40 red and 10 blue M&M's; one jar has 25 green and 25 blue M&M's; and one jar has 30 orange and 20 blue M&M's.
If you randomly pick a jar and then randomly pick an M&M from that jar, what is the probability you will pick a green M&M?
1/6
What are the eigenvalues of the matrix
[[2,3],[2,1]]
Suppose A, B, and C are all n-by-n matrices where the determinant of A is 6, the determinant of B is 12, and C satisfies the equation
det(AB^{-1})=det(A^{-1}C)
What is the determinant of C?
3
How many ways are there to place n indistinguishable marbles into m distinguishable urns?
((n+m-1),(n)) = ((n+m-1),(m-1)) = ((n+m-1)!)/(n!(m-1)!)
This quadrennial award given for outstanding contributions in mathematics was first won by Lars Ahlfors and Jesse Douglas in 1936.
The Fields medal
Suppose the probability a randomly selected number in the unit interval [0, 1] lies in a subinterval (a, b) is b - a.
If a number is randomly selected, what is the probability that it is a rational number?
0
What are the real eigenvalues of a (non-trivial) rotation matrix?
Rotation matrices have no real eigenvalues.
Suppose 2 + 3i is a root of a quadratic polynomial with real coefficients. What is the other root?
2 - 3i
How many subgroups are there of
ZZ_11?
Two: the trivial group and the entire group.
This 19th century German mathematician is sometimes referred to as the Prince of Mathematics.
Gauß
Suppose that 70% of people with the flu have a sore throat, and 15% of people without the flu have a sore throat. If 10% of people in a given population have the flu, what is the probability a randomly selected person has a sore throat?
Let E be the event the randomly selected person has a sore throat, and F the event the person has the flu. By the law of total probability,
Pr(E) = Pr(E|F)Pr(F) + Pr(E|Fc)Pr(Fc)
= 0.7 * 0.1 + 0.15 * 0.9
= 0.07 + 0.135 = 0.205
What are the geometric multiplicities of the eigenvalues of the following matrix?
[[2,1,0,0,0],[0,2,1,0,0],[0,0,2,0,0],[0,0,0,2,1],[0,0,0,0,2]]
The only eigenvalue is 2 which has geometric multiplicity 2.
What is the area of the shaded region below?
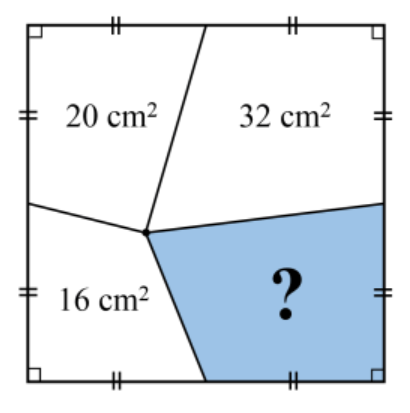
28 cm2
How many surjective functions exist from a set of cardinality m to a set of cardinality n > m?
0
Founded in modern day Eswatini, this artifact is comprised of tally marks etched on the fibula of a baboon. It is also considered to be the earliest mathematical artifact.
The Lebombo Bone
If ten points are randomly selected in a 3-by-3 square, what is the probability at least two points are no more than distance √2 from one another?
1
What is the minimum number of real eigenvalues a real 5-by-5 matrix can have?
Any real (2n+1)-by-(2n+1) must have at least one real eigenvalue.
A rubber band is stretched around three circles of diameter 3 as in the figure below. What is the length of the rubber band?
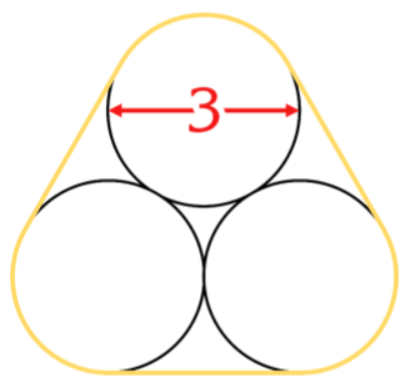
9 + 6 pi
How many injective functions exist from a set of cardinality m to a set of cardinality n > m?
(n!)/((n-m)!) = n \cdot (n-1) \cdot (n-2) \cdot \ldots (n-m+1)
This university employed several famous mathematicians including Gauss, Riemann, Hilbert, Noether, and Klein.
Universität Göttingen
Let X and Y be discrete random variables with the following joint probability mass function:
p(x, y) = {(1/4,if(x,y)\in{(1,1),(2,2),(3,3),(4,4)}),(0,otherwise):}
What is the covariance of X and Y?
Cov(X,Y) = \mathbb{E}[XY] - \mathbb{E}[X]\mathbb{E}[Y] = 15/2 - (5/2)^2 = 5/4
The derivative is a linear operator on the set of all smooth functions defined on the entire real line. What are the eigenvalues and eigenvectors of this operator?
Every real number λ is an eigenvalue with eigenvectors eλx.
Compute the following limit:
lim_{n\to\infty}\sum_{i=1}^n\sqrt{1 - (-1 + (2i)/n)^2}2/n
pi/2