Concepts
Probability
Count This
Probably More Probability
Distributions
100
Consider two independent events C and D. P(C nn D) = P(C) + P(D) . True or False? If false, provide a correction.
False. Multiply!!
100
What is the probability of getting a total of 7 or 11 when a pair of fair dice is tossed?
2/9
100
In how many different ways can a True-False test consisting of nine questions be answered?
512
100
Three cards are drawn without replacement from an ordinary deck. Find the probability that exactly two of the cards are red.
13/34
100
Given the following probability mass function, construct the cumulative distribution function, F(X).
| x | 0 | 1 | 2 | 3 | 4 |
| f(x) | 0.41 | 0.37 | 0.16 | 0.05 | 0.01 |
F(x)={(0,if x<0),(0.41,if 0<=x=1), (0.78,if 1<=x<2), (0.94,if2<=x<3), (0.99,if3<=x<4), (1,ifx>=4):}
200
If A and B are mutually exclusive, then P(A|B) = P(A). True or False, if False, provide a correction.
False, the intersection would be empty, so the resulting probability is 0.
200
Suppose that in a senior college class of 500 students it is found that 210 smoke, 258 drink, 216 eat between meals, 122 smoke and drink, 83 eat between meals and drink, 97 smoke and eat between meals, and 52 engage in all three. What is the probability a student selected at random smokes but does not drink?
88/500 = 0.176
200
How many distinct permutations can be made from the letters in the word INFINITY?
3360
200
Given P(A' and B') = 0.3, and P(A and B') = 0.4, find P(B).
0.3 (use venn diagram!)
200
Compute F(X) for the following pdf:
f(x)={(3x^-4,if x>1),(0,elsewhere):}
F(x)={(0,if x<1),(1-x^-3,ifx>=1):}
300
The expected value of a random variable X, E[X], gives the value of the random variable we're most likely to see. True or False? If false, provide a correction.
False! This is a measure of the mean or average, the central tendency for a random variable. (the mode is most likely value).
300
A class in advanced physics is composed of 10 juniors, 30 seniors, and 10 graduate students. The final grades show that 3 of the juniors, 10 seniors, and 5 graduate students received an A grade. If a student is chosen at random and is found to have earned an A, what is the probability that he or she is a senior?
10/18 = 0.5555
300
A young boy asks his mom to get 5 compact discs (CDs) from his collection of 10 country and 5 rock CDs. How many ways are there for his mother to get 3 country and 2 rock CDs?
120*10=1200 ways
300
A manufacturing firm employs three analytical plans for the design of a particular product. Plans 1, 2, and 3 are used for 30%, 20%, and 50% of the products respectively. The defect rate for the procedures is 1%, 3% and 2%, respectively. If a randomly selected product was observed and found to be defective, which plan was most likely used and thus responsible?
The conditional probability of a defect given plan 3 is the largest of the three.
3:0.526
2:0.316
1:0.158
300
Two tire-quality experts examine a stack of tires and assign a quality rating to each tire on a 3-point scale. Let X denote the rating given by expert A and Y the rating by expert B. The following table gives the joint distribution, use it to compute
mu_Y
| Y | ||||
| 1 | 2 | 3 | ||
| 1 | 0.10 | 0.05 | 0.02 | |
| X | 2 | 0.10 | 0.35 | 0.05 |
| 3 | 0.03 | 0.1 | 0.20 |
2.04 (the mean of X is 2.16)
400
If F(0) = 1/16 for 0<= x < 1, and F(1) = 5/16 for 1<= x < 2, what is f(1)?
4/16 = 1/4
400
Find the probability of randomly selecting 4 good quarts of milk in succession from a cooler containing 20 quarts of milk, of which 5 have spoiled.
91/323 = 0.2817.
400
In how many different ways can 5 different trees be planted in a circle?
4! = 24
400
When playing American roulette, the attendant spins a marble that lands in one of the 38 equally spaced slots in a revolving table. The slots numbered 1 to 36 are colored red and black (see image). Two slots are green, 0 and 00, and are not considered as even or odd. Find the probability that the marble will land in a red or even number. (fyi: 28 is usually black, but not here---this is just for fun)
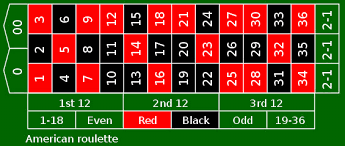
27/38
400
A continuous random variable W has the density function
f(w)={(e^-w,if w>0),(0,elsewhere):}
Find the expected value of g(W) = e^((2w)/3)
int_0^infty g(w)f(w)dw = int_0^infty e^(-w/3)dw=3
500
Suppose event A can be partitioned into three subsets B1, B2, and B3. Write the right-hand side of the equation to find P(B3|A) using Bayes Rule.
Numerator: P(B3)*P(A|B3)
Denominator: P(B1)*P(A|B1) + P(B2)*P(A|B2) + P(B3)*P(A|B3)
500
A manufacturing firm employs three analytical plans for the design of a particular product. Plans 1, 2, and 3 are used for 30%, 20%, and 50% of the products respectively. The defect rate for the procedures is 1%, 3% and 2%, respectively. What is the probability a randomly selected product is defective?
0.019
500
How many ways are there that no two students will have the same birthdate in a class of size 60? (assume 365 days in a year)
365 P 60 (365*364*363* ... *306)
500
A grand prize is behind one of three doors, A, B, or C. Suppose you randomly picked door A. The game show host opens door B and showed you there was no prize behind it. The host now offers you the option of sticking with door A or switching to C. What should you do and why?
Switch to door C. You were more likely to pick the wrong door at the beginning than the correct one.
500
Suppose that X and Y have the following joint probability function. Find the expected value of g(X,Y) = XY^2
| X | |||
| 2 | 4 | ||
| 1 | 0.10 | 0.15 | |
| Y | 3 | 0.20 | 0.30 |
| 5 | 0.10 | 0.15 |
35.2