This is Normal
Discrete Games
Not Discrete Games
Distribute This
And Sample This
100
Suppose X has a normal distribution with \mu = 300 and \sigma = 50 . What z-value would correspond to X = 362?
z = \frac{362-300}{50} = 1.24
100
From a standard 52 card deck of playing cards, what is the probability of getting dealt a hand of 5 cards, of which 3 are red and 2 are black?
0.3251
100
Find the P(Z<-1.33).
0.0918
100
In certain rule variations of the game Monopoly, a player remains stuck in Jail (once placed there) until they use a "Get of Jail Free" card or role doubles (a pair) from two standard 6-sided dice. What distribution models the event of trying to role a pair to get out of jail?
This is geometric (or negative binomial with k = 1) since we only need the first success, with probability p = 1/6.
100
Given the following dataset: 16, 10, 4, 12, 4, 10, 4, 10, 9, 3. Give the sample median and mode.
The median is the average of the two middle values. so \tilde{x} = 9.5 . Both 4 and 10 appear three times, so the modes are: 4, 10.
200
Find
P(Z<-1.24).
1 - 0.8925 = 0.1075.
200
In a popular video game, L.O.L., a critical strike is a damage effect that deals bonus damage to your opponent. What is the probability that at least two of the next four attacks are critical strikes assuming a constant critical strike chance of 40%?
This binomial, with n = 4 and p = 0.40. The desired probability is 1-0.4752 = 0.5248
200
Suppose X follows a continuous uniform distribution from 1 to 5. Determine P(X>2.5|X<=4).
1/2.
200
For a random engineering student that earned a C in Calculus 1, suppose the probability of passing Stat 3611 is 0.05. The student must pass Stat 3611 before taking their major courses. What distribution would be most appropriate if we're interested in the number of semesters before the student can take their major courses?
The idea here is that we're looking for the first success, so this is Geometric with p = 0.05.
200
Engineers are quite certain that the variance of the weight of product is 2 ounces. Experiments are conducted on two different production machines, both with samples of 49. The sample averages for A and B are 9.8 and 10.1 ounces respectively. Assuming that the true means for both machines are the same, what is the distribution of the difference of sample means, bar X_B - bar X_A ?
The difference of sample means is zero if we assume they're equal. Since the variance and sample sizes are the same for both, the sum of the variances is just 2*(2/49).
(bar X_B - bar X_A )~N(mean = 0, var = 4/49)
300
Suppose X has a normal distribution with \mu = 300 and \sigma = 50 . Find P(300<X<362)
Since the mean of X is 300, this is just:
P(Z<1.24) - 0.50 = 0.8925-0.50 = 0.3925
300
During dinner rush, the telephone lines for a Chinese Take-Out restaurant may become near capacity and customers phone calls may be met with a busy signal. Suppose p = 5% is the connection probability during a dinner rush. What is the probability that 5 attempts are necessary for a successful call to place your order?
(0.05)(0.95)^4 = 0.041
300
After extensive testing, it is determined that the time in years before a major repair for a washing machine brand follows an exponential distribution with a mean of 4 years. What is the probability that a given machine does not require a repair until after year 6?
1 - P(T<=6) = e^(-3/2) = 0.2231
300
The average number of field mice in a 5 acre wheat field is estimated to be 12. What distribution ( and parameters) would be best used to answer: Find the probability that fewer than 7 field mice are found on 2 of the next 3 acres inspected.
Poisson. \lambda * t = \mu = 7.2 -> P(X = x) = \frac{e^(-7.2)(-7.2)^x}{x!}
300
The tar contents, in milligrams, of a selection of cigarettes selected at random are: 9.9, 7.3, 11.8, 16.6, 11.7, 16.5, 12.3, and 10.4. For the sample, calculate the sample mean and the sample variance.
\bar{x} ~~12.06
s^2 ~~ 10.09
\text{ see thm. 8.1 for s^2
400
The average grade for an exam is 74, and the standard deviation is 7. If 12% of the is given A's and the grades are curved to follow a normal distribution, what is the lowest possible A and the highest possible B?
We need a z-value that leaves 12% area to the right, or 88% to the left. The closest is 1.18. Converting from Z to X we find the cut-off at 7(1.18)+74 = 82.26. So an A is 83, and B is 82.
400
Ten is the average number of oil tankers arriving each day at a certain port. The facilities at the port can handle at most 15 tankers per day. What is the probability that on a given day tankers have to be turned away?
Via Poisson Table:
P(X>15) = 1 - P(X<= 15) = 1-0.9513 = 0.0487
400
Given a normal distribution with a mean of 30 and a s.d. of 6, find the two values of X that contain the middle 75% of the normal curve area.
We want x-values so that
P(x_1<X<x_2) = 0.75.
By symmetry, this leaves 12.5% area in either tail. If this was standard normal, we'd see the left bound is -1.15, so now we convert to X.
(x_1 - 30)/6 = -1.15 -> x_1 = 23.1, \text{similarly } x_2 = 36.9
400
Evaluate:
int_45^62 1/sqrt(200 \pi) e^(-1/200 (x-50)^2)dx
X has a pdf that is normal with mean 50 and variance = 100.
=> P(-0.5<Z<1.2) = 0.8849-0.3085
0.5764
400
Suppose X is a R.V. with a mean of 2000 and a standard deviation of 300. If we take a sample of size 100, what is the probability that the sample average is between 1962.50 and 2000?
Via CLT, this is equivalent to P(-1.25<Z<0) = 0.50--.1056 = 0.3944.
500
A process yields 10% defective items. If 100 items are randomly selected from the process, what is the probability that the number of defectives exceeds 13?
Approximate with normal curve with mean = np and variance = npq. With continuity correction:
1-P(Z<= (13.5-10)/3) = 0.120
500
For $2, you can pick five different numbers from 1–69 and one Powerball number from 1–26. To win the $50,000 prize, one must get four of the five white numbers and the Powerball. What is the probability of winning exactly the $50,000 prize?
\frac{((5), (4))((64), (1)) ((1), (1)) ((25), (0))}{((69), (5)) ((26),(1))} ~~0.000001096
500
Statistics released by the National Highway Traffic Safety Administration show that on an average weekend night, 1 out of every 10 drivers on the road is drunk. If 400 drivers are randomly checked next Saturday night, what is the probability the number of drunk drivers is at least 35 but less than 47?
We want P(35<= X <47) where X is binomial with n = 400 and p = 0.10. Approximate with a normal dist. with mean = 40 and variance = 36. Taking care with the strict inequality on the right and the cty correction: P(-0.9166 <= Z <= 1.0833) ~~0.6811
500
Identify and estimate parameters for all of the distributions shown in the following:
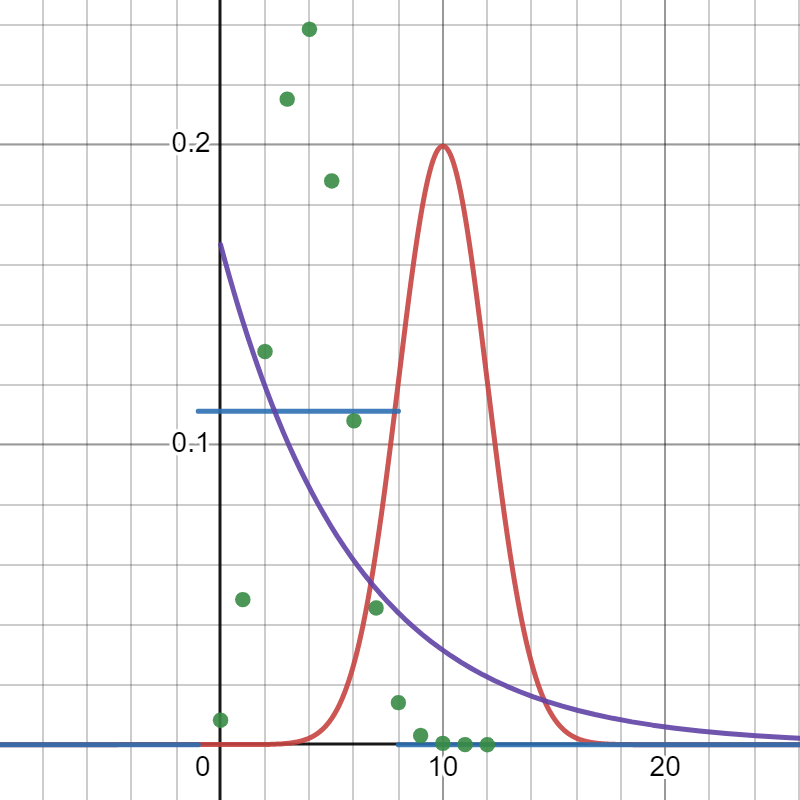
In Red: n(\mu = 10, \sigma ~~ 2). In Blue: Continuous Uniform on [-1, 8]. In Green, Binomial with n = 12 and p = 1/3 (note the mean, np is the peak at 4). Purple is exponential ( \beta = 6 but it's hard to estimate that.
500
Engineers are quite certain that the variance of the weight of product is 2 ounces. Experiments are conducted on two different production machines, both with samples of 49. The sample averages for A and B are 9.8 and 10.1 ounces respectively. Assuming that the true means for both machines are equal, what is the probability that the difference of sample means, \bar{X_B} - \bar {X_A} >=0.3 ?
Using them 8.3, this is normal with mean = 0 and variance 4/49. Rounded to 4 places, this is about 0.1469.