Normal Distributions & Probabilities (5.1-5.3)
Central Limit Theorem and Sampling Distributions (5.4)
Confidence Intervals for Means (6.1-6.2)
Confidence Intervals for Proportions, St. Dev & Variance (6.3-6.4)
100
- Select the correct excel formula that would be used to find the area to the left of z=-0.34 on the standard normal curve. (2 points)
A
100
The central limit theorem stats that given any population distribution, the distribution of sample means will be approximately normal given that the sample size is at least _______.
30
100
For the same sample statistics, which level of confidence would produce the widest confidence interval? Explain your reasoning.
C
100
A wildlife biologist wishes to estimate, with 90% confidence, the population proportion of a certain species of birds that migrate south for the winter. The estimate must be accurate within 2% of the population proportion. What is the minimum sample size needed assuming that no prior information is available?
1692
200
Use an attached table to find the area between z=-2.13 and z=1.54 on the standard normal curve. Round to three decimal places.
0.922
200
The weights of a certain breed of adult dogs are normally distributed, with a mean of 55 pounds and a standard deviation of 9 pounds. Random samples of size 20 are drawn from the population. Use the central limit theorem to find the sampling mean and standard error of the sampling distribution. Round to two decimal places.
sampling mean: 55
standard error: 2.01
200
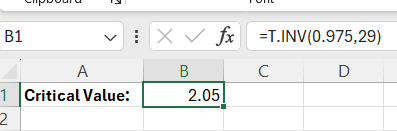
Select the correct excel formula that would be used to find the critical value for a 99% confidence interval when the sample size is 35.
D
200
In a survey of 1500 college students, 900 say they prefer online classes over in-person classes. a. Construct a 99% confidence interval for the population proportion of college students who prefer online classes. Write a sentence describing the confidence interval.
(0.5674, 0.6326)
We can say with 99% confidence that the true mean population proportion of college students who prefer online classes over in-person classes is between 56.74% and 63.26%.
300
Last semester, the scores for the statistics final exam were normally distributed with a mean of 78.4% and a standard deviation of 8%. Find the probability of a student scoring less than 65%.
0.047
300
Find the minimum sample size to estimate the population mean for a normal distribution when c=0.9, sigma = 4.3 and E=1.2.
35
300
The weights (in pounds) of 21 randomly selected adult elephants have a sample standard deviation of 250 pounds. Assuming the weights of adult elephants are normally distributed, construct a 95% confidence interval for the population standard deviation. Explain the confidence interval in a sentence.
(191.26, 361.01) pounds
We can say with 95% confidence that the true mean weight of adult elephants is between 165.07 and 477.40 pounds.
400
A botanist is studying the growth of a particular type of plant. The heights of these plants are normally distributed with a mean of 15 inches and a standard deviation of 2.5 inches. Find the height x corresponding to the z-score of 0.8.
17 inches
400
A biologist is studying the weights of a sample of 50 adult turtles. The sample has a mean weight of 12 pounds. Assume the population standard deviation is 2.8 pounds. Construct a 95% confidence interval for the population mean and write a sentence. Round to two decimal places.
(11.22, 12.78) pounds
We can say with 95% confidence that the true mean population weight of adult turtles is between 11.72 and 13.28 pounds.
500
A researcher randomly selects 30 Lake Michigan College students and measures the mean time they spend on homework each week. The sample mean was 12.5 hours and the sample standard deviation was 3.2 hours. a. Use the Excel screenshot below to calculate a 95% confidence interval. Round to two decimal places.
Write a sentence explaining the confidence interval.
(11.31, 13.69) hours
We can say with 95% confidence that the true population mean time LMC students spend on homework each week is between 11.31 and 13.69 hours.