Solving Systems of Linear Equations by Graphing
Systems of Linear Inequalities
Writing systems of equations and inequalities
100
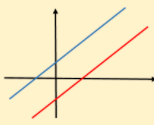
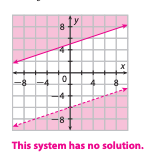
Fill in the Blank: This system of equations has _____ solutions. (10 seconds)
No Solutions
100
Fill in the blank: An inequality with < or > has a ___________ line.
Broken or dashed line because points on the line are not included in the solutions.
100
(10 seconds) Fill in the blank: When writing a system of equations or inequalities, you should always ___________ your variables.
Define your variables
example
x= # of students
y = # of teachers
200
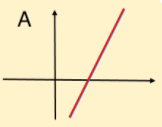
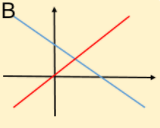
Which graph shows one solution? A or B? (10 seconds)
B
200
(20 secs) Is the point (1,3) a solution to this system of inequalities?
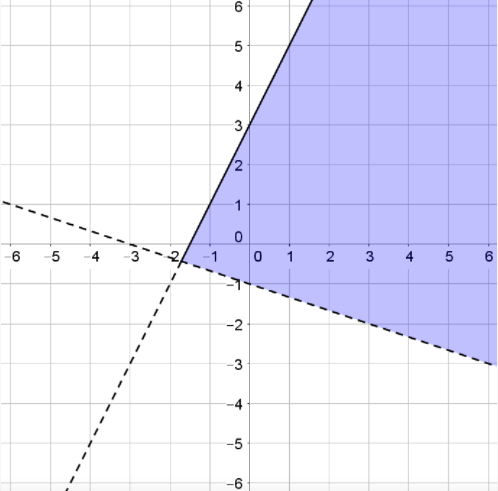
Yes, it is in the double shaded region so it is a solution to both inequalities.
200
(1 minute) Ashley has two jobs: mowing lawns and babysitting. She earns $10 per hour mowing lawns (x) and $8 per hour babysitting (y). She wants to earn exactly $160 next week.
Write a system in standard form (ax+by=c) to represent this situation.
10x+8y=160
300
(1 Minute) Use Desmos to solve the system of linear equations by graphing:
y = 2x + 5
y=1/2 x-1
(-4,-3)
300
(20 secs) Is the point (0,3) a solution to this system of inequalities?
Yes, it is in the double shaded region and falls on a solid line so it is a solution to both inequalities
300
(1 minute) Ashley has two jobs: mowing lawns and babysitting. She earns $10 per hour mowing lawns (x) and $8 per hour babysitting (y). She wants to earn at least $160 next week.
Write a system in standard form to represent this situation.
10x+8y>=160
400
Use desmos to solve the system of linear equations by graphing:
x + y = 7
y = x + 3
(1 minute)
(2,5)
400
(20 secs) Is the point (0,-1) a solution to this system of inequalities?
No, it is in the double shaded region but it falls on a dashed or broken line so it is not a solution to both inequalities.
400
(3 mins) Start-up costs: Jordan and Payton can spend up to $45 that they have saved to start their business. They are planning to sell flashlights and emergency blankets. They have a supplier that they can purchase these items from. Their cost will be $3 per blanket and $5 per flashlight.
Be sure to define the variables.
3b+5f<45
b = # of blankets
f = # of flashlights
500
(1 min) Describe and correct the error in the explain of the system of linear equations.
y = -2x + 4
y = -2x + 6
The lines have the same slope and different y intercepts so there are infinitely many solutions.
The lines have the same slope but different y-intercepts so therefore they are never going to intersect = No Solution.
Different slope and different or same y-intercept = one solution.
Same slope and same y-intercept = infinite solutions.
500
(2 mins) Graph the inequality on Desmos, how would you describe the solution to the system:
y ≥1/3 x+5
y<1/3 x-6
500
Income Requirements: Jordan and Payton are planning to sell the blankets for $6 each and sell the flashlights for $10 each. Their parents have told them that if they are not able to make more than $180, then they need to do something else, so they have made it a goal to make more than $180.
Be sure to define the variables.
6b+10f>180
b = #of blankets
f = # of flashlights