What is the center and radius of the following circle?
(x-6)^2+(y+1)^2=4
Center: (6,-1)
Radius: 2
(x-h)^2=4p(y-k)
Based on the above equation, how do you know when a parabola opens up or down?
'p' or '4p' is positive when a parabola opens up, negative when a parabola opens down.
Solve the following system of equations:
y=x^2-4x+12
y=4x-4
x^2-4x+12=4x-4
x^2-8x+16=0
(x-4)(x-4)=0
x=4
y=4(4)-4=12
Solution(s): (4,12)
Solve the following system of equations:
-3x+2y=1
x-5y=-9
Multiply second equation by 3 to eliminate Xs
-3x+2y=1
3x-15y=-26
-13y=-26
y=2
Substitute y with 2 in either equation to solve for x
x-5(2)=-9
x-10=-9
x=1
Solution: (1,2)
What is the equation of this circle?
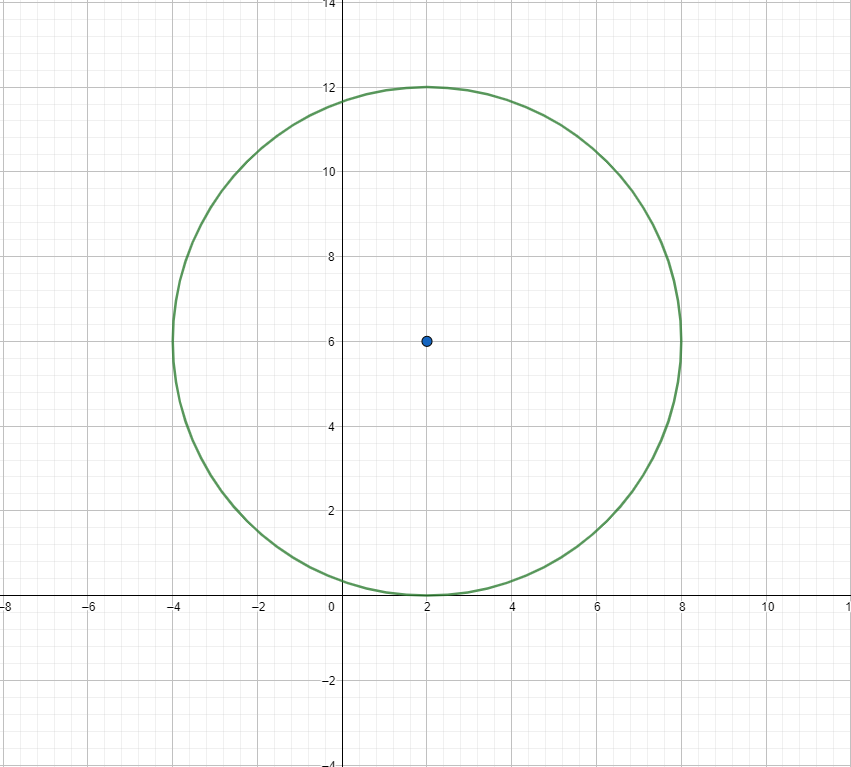
(x-2)^2+(y-6)^2=36
A parabola has a focus at (2,5) and a directrix at y=1.
What are the coordinates of the vertex AND what is the 'p' value?
Vertex: (2,3)
'p' value: 2
Solve the following system of equations:
y=x^2-6x+1
y=-5x+1
x^2-6x+1=-5x+1
x^2-x=0
x(x-1)=0
x=0, x=1
y=-5(0)+1=1
y=-5(1)+1=-4
Solution(s): (0,1),(1,-4)
What is the center and radius of the following circle?
y^2+8y+x^2+4x-5=0
y^2+8y+?+x^2+4x+?=5+?+?
y^2+8y+16+x^2+4x+4=5+16+4
y^2+8y+16+x^2+4x+4=25
(y+4)^2+(x+2)^2=25
Center: (-2,-4)
Radius: 5

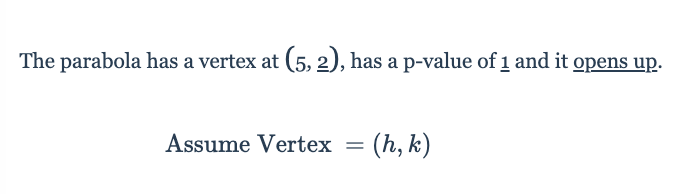
Equation:(x-5)^2=4(y-2)
Solve the following system of equations:
(x+2)^2+(y)^2=36
y=x-4
(x+2)^2+(x-4)^2=36
(x+2)(x+2)+(x-4)(x-4)=36
x^2+2x+2x+4+x^2-4x-4x+16=36
2x^2-4x+20=36
2x^2-4x-16=0
2(x^2-2x-8)=0
2(x-4)(x+2)=0
x=4,x=-2
y=(4)-4=0
y=(-2)-4=-6
Solution(s): (4,0),(-2,-6)
Solve the following system of equations:
2x+y-z=-5
-3x-2y+z=5
6x-3y-z=-13
Add equations 1 and 2, along with 2 and 3 to eliminate the Zs
A) -x-y=0
B) 3x-5y=-8
Multiply equation A by 3 to eliminate the Xs
-3x-3y=0
3x-5y=-8
-8y=-8
y=1
Substitute y with 1 in equation A or B to solve for X.
-x-1=0
-x=1
x=-1
Substitute x and y with -1 and 1 in any of the three original equations to solve for Z
z=4
Solution:(-1,1,4)
Identify the center and the radius:
y^2+x^2+9-6y-8x=0
x^2-8x+y^2-6y+9=0
x^2-8x+y^2-6y=-9
x^2-8x+?+y^2-6y+?=-9+?+?
x^2-8x+16+y^2-6y+9=-9+16+9
(x-4)^2+(y-3)^2=16
Center: (4,3)
Radius: 4
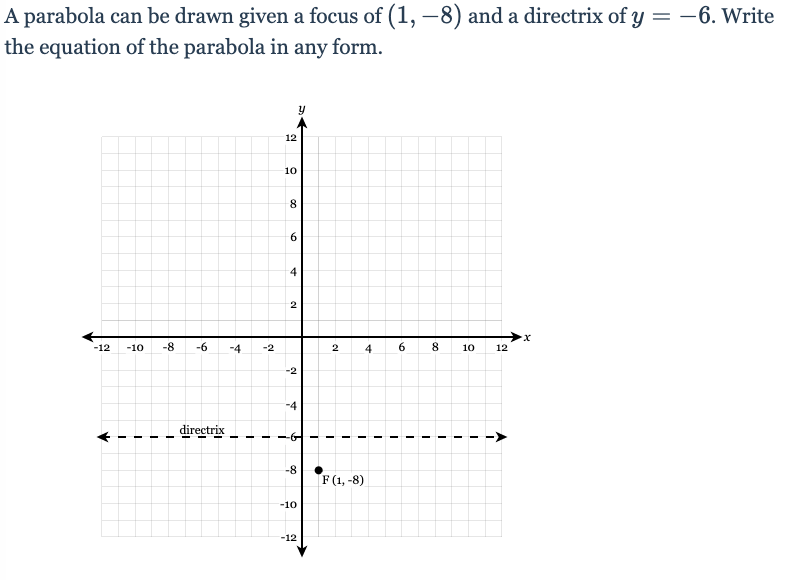
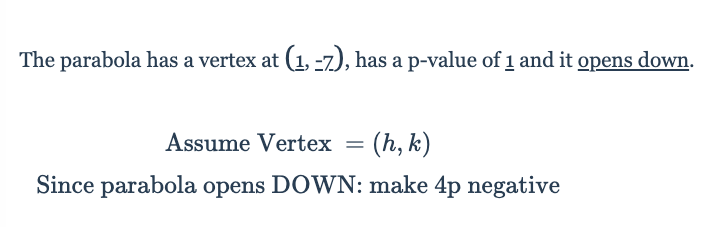
Equation: (x-1)^2=-4(y+7)
Solve the following system of equations:
y=x^2-4x+3
y=-2x-7
x^2-4x+3=-2x-7
x^2-2x+10=0
x^2-2x+(-1)^2=-10+(-1)^2
(x-1)^2=-9
x-1=pmsqrt(-9)
x=1pm3i
Solution(s): No real solutions
Identify the center and the radius:
-y^2-6y+2x-x^2=-9
y^2+6y-2x+x^2=9
y^2+6y+?+x^2-2x+?=9+?+?
y^2+6y+9+x^2-2x+1=9+9+1
(y+3)^2+(x-1)^2=19
Center: (1,-3)
Radius: sqrt(19)
Write the equation of the parabola in standard (4p) form:
x^2-6x-16y-71=0
x^2-6x=16y+71
x^2-6x+?=16y+71+?
x^2-6x+9=16y+80
(x-3)^2=16(y+5)
Solve the following system of equations:
x^2+4x+y^2-2y-20=0
y=-x-2
x^2+4x+?+y^2-2y+?=20+?+?
x^2+4x+4+y^2-2y+1=20+4+1
(x+2)^2+(y-1)^2=25
(x+2)^2+(-x-2-1)^2=25
(x+2)(x+2)+(-x-3)(-x-3)=25
x^2+2x+2x+4+x^2+3x+3x+9=25
2x^2+10x+13=25
2x^2+10x-12=0
2(x^2+5x-6)=0
(x+6)(x-1)=0
x=-6,x=1
y=-(-6)-2=4
y=-(1)-2=-3
Solution(s): (-6,4),(1,-3)
Solve the following system of equations:
2x-3y+4z=17
-x+4y-3z=-17
5x-3y+8z=27
Multiply equation #2 by 5 and add to equation 3
Multiply equation #2 by 2 and add to equation 1
A) 17y-7z=-58
B) 5y-2z=-17
Multiply equation A by -2 and multiply equation B by 7. Then add the resulting equations.
y=-3
Substitute y with -3 in equation A or B and solve for Z.
5(-3)-2z=-17
-15-2z=-17
-2z=-2
z=1
Substitute y and z with -3 and 1 in any of the original equations to solve for X.
-x+4(-3)-3(1)=-17
-x-12-3=-17
-x-15=-17
-x=-2
x=2
Solution: (2,-3,1)
In a car factory, 6 machines can make 6 wheels in 6 minutes. How long will it take 30 machines to make 30 wheels?
30 machines will make 30 wheels in 6 minutes.