Graphing
More Graphing
Substitution
Vocabulary
100
y = 2x + 2
y = x - 1
(3,-4)
100
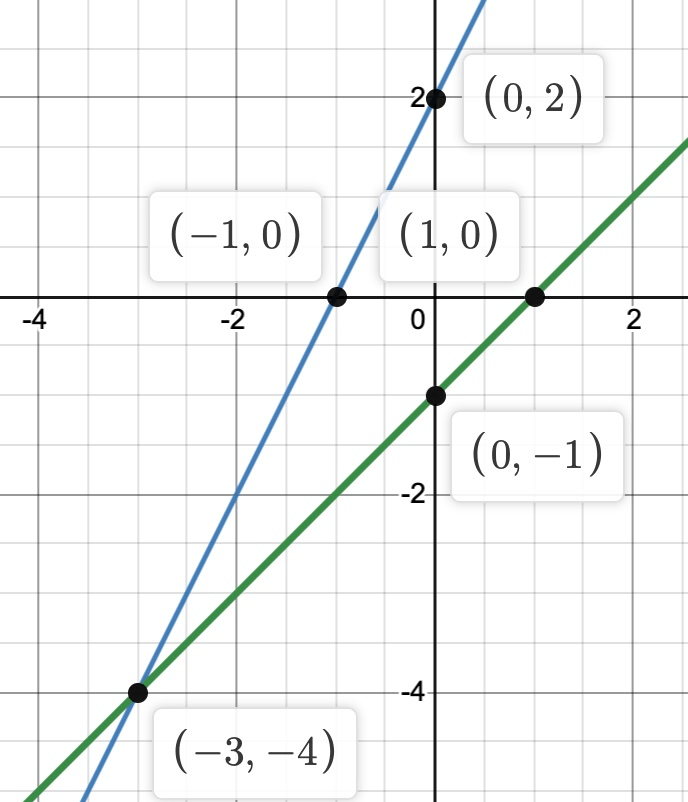
y= x+8
y= -3/2 x-2
(-4,4)
100
y = 2
3x + 2y = 10
(2,2)
100
what are the 3 methods of solving systems of equations
elimination
graphing
substitution
200
y = 2x + 5
y = x + 3
(-2,1)
200
y=2x-2
y=-x+7
(3,4)
200
y = x + 1
2x + y =10
(3,4)
200
there are two graphs on the same coordinate plane
systems of equations
300
3x - 2y = 8
x + y = 6
(4,2)
300
y= x+8
y=−3x−4
(-3,5)
300
y = 5x - 1
2y = 3x + 12
(2,9)
300
How can you tell if a linear system has infinitely many solutions?
the equations are the same and the lines lie on top of each other
400
y = 1/2x + 2
y = 1/4x + 4
(8,6)
400
y=x+3
2x+y=−3
(−2,1)
400
2x - 3y = -2
y= -4x + 24
(5,4)
400
what does it mean when the lines are parallel or they have the same slope and different y-intercepts or when you solve the equations and get a false statement with no variables remaining.
no solution
500
4x - 5y = 15
8x + 5y = 45
(5,1)
500
y=2x−3
x+y=−6
(−1,−5)
500
x + y = 10
-y = 5 + x
no solution
500
The method of solving equations where you solve for one variable and plug into solve the other
substitution