Methods & Solutions
Graphing
Substitution
Definitions
100
What are the three practiced methods used for solving systems of equations?
"the Graphing Method, the Substitution Method, and the Elimination Method"
100
Solve this system graphically:
y = 2x
y = 3x - 3
(3,6)
100
Solve this system using Substitution:
y = x + 1
x + y = 9
(4,5)
100
The answer of a systems of linear equations.
the solution
200
Is the ordered pair (- 2, 8) a solution of
8x + 2y = 0
x - 2y = -18
YES
200
What is the solution of this systems of equations?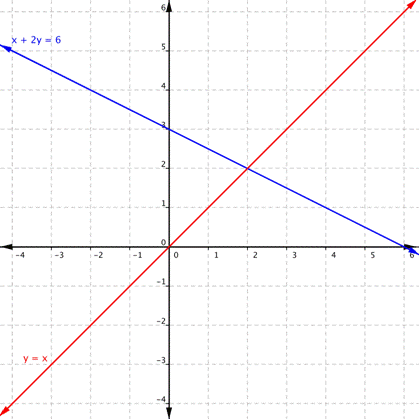
(2,2)
200
Solve this system using Substitution:
a = 3b + 1
5b - 2a = 1
(-8, -3)
200
The two lines have the same slope and different y-intercept. The number of solutions for this type of systems of equations is:
none
300
In what method would you replace a variable with something of equal value?
Substitution
300
Solve this system graphically:
y = 2x + 2
y = -x + 5
(1,4)
300
The solution of the following system of equations:
y=-3
y=6x+3
(-1,-3)
300
The format used to write a solution of a system of linear equations.
an ordered pair
(x,y)
400
Which method is the most efficient method to solve this system of linear equations?
y=-2x+3
y=4
"the Substitution Method"
400
Solve this system graphically:
x + y = -7
x - y = 1
(-3, -4)
400
Solve the following system of equations using substitution.
y=x+6
x+2y=6
(-2, 4)
400
The lines have the same slope and same y-intercept. What is the number of solutions for this type of system of equations?
infinitely many
500
Is the ordered pair (-1,2) a solution of x-y=-3 and 2x+y=0?
YES
500
What is the solution to this system of equations?
NO SOLUTION
500
The solution of the following system of equations:
y=-3x
-3x+3y=0
What is "(0,0)"?
500
A one word expression to describe a system of equations that has no solution, but is not the word parallel.
Inconsistent