Systems with Graphs
Solving by Substitution
Solving by Elimination
Mixed
100
What is the solution?
(-1,1)
100
Solve the systems of equations:
-3x + 4y = -2
y = -5
(-6, -5)
100
Solve the systems of equations:
14x + 2y = 26
-14x - 6y = -50
(1, 6)
100
What is the "answer" to a systems of equation?
and ordered pair, where the two lines intersect (or don't if they are parallel). Any form of this answer is correct. Essentially: the point where two lines cross
200
How many solutions are there?
No Solutions
200
Solve the systems of equations:
-5x - 5y = 10
y = -4x -17
(-5, 3)
200
Solve the systems of equations:
-3x - 5y = 2
3x + 5y = 7
No Solution
200
What are the three ways to solve a system of equations?
graphing, substitution, or elimination
300
Solve Using Graphing:
y = 5/3x + 2
y = -3
300
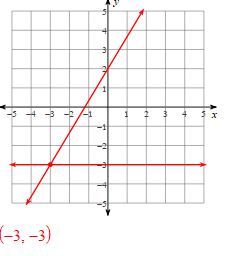
Solve the systems of equations:
y = -2x - 9
3x -6y = 9
(-3, -3)
300
Solve the systems of equations:
-6x - 10y = 4
6x + 10y = 0
No Solution
300
What does it mean when you get an answer such as 0=2, or no solution?
It means the lines are parallel. Since they never intersect there are no solutions to the system.
400
How many solutions are there?
Infinitely Many Solutions
400
Solve the systems of equations:
-8x - 5y = -24
-x + y = 10
(-2, 8)
400
Solve the systems of equations:
-3x - 24y = -66
3x + 4y = -14
(-10, 4)
400
What does it mean when a solution to a system of equation is a true statement, such as 7=7, or infinite solutions?
These are the same exact line, therefore they have
Infinite Solutions since every point on the line satisfies both equations.
500
Solve the systems of linear equations by graphing:
500
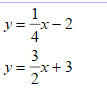
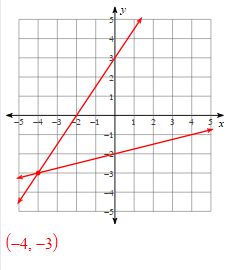
Solve the systems of equations:
-8x + y = -7
16x - 2y = 14
Infinitely Many Solutions
500
Solve the systems of equations:
-15x + 6y = -36
8x - 6y = 22
(2, -1)
500
How you tell if the following equations have one, no, or infinite solutions without solving the system?
y = -5x -12
y = 1/2 x + 3
If the lines have different slopes, then the lines intersect. Therefore, there is only one Solution.