Systems with Graphs
Solving by Substitution
Solving by Elimination
Best Strategy
Random
100
What is the solution?
(-1,1)
100
Solve the systems of equations:
-3x + 4y = -2
y = -5
(-6, -5)
100
Solve the systems of equations:
-5x + 6y = 2
-8x - 7y = -30
(2, 2)
100
What strategy would be best?
14x + 2y = 26
-14x - 6y = -50
Elimination because the coefficients on x are the same number with opposite signs
100
Is the given point a solution to the system of equations?
Point: (1,-3)
x + 2y = -5
3x + y = 0
Yes
200
Solve using Graphing
y= 2x + 1
y= -x + 7
(2, 5)
200
Solve the systems of equations:
-5x - 5y = 10
y = -4x -17
(-5, 3)
200
Solve the systems of equations:
-3x - 5y = 2
3x + 5y = 7
No Solution
200
What strategy would be best?
y = 4x + 3
y = -2x + 1
Graphing or Substitution because both equations are in slope-intercept form
200
The school that Stefan goes to is selling tickets to a choral performance. On the first day of ticket sales the school sold 3 senior citizen tickets and 1 child ticket for a total of $38. The school took in $52 on the second day by selling 3 senior citizen tickets and 2 child tickets. Find the price of a senior citizen ticket and the price of a child ticket.
Senior Citizen Ticket $8
Child Ticket $14
300
Solve Using Graphing:
y = 5/3x + 2
y = -3
300
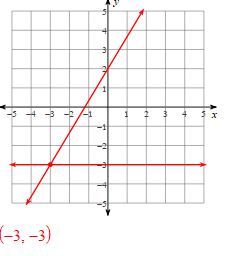
Solve the systems of equations:
y = -2x - 9
3x -6y = 9
(-3, -3)
300
Solve the systems of equations:
-6x - 10y = 4
6x + 10y = 0
No Solution
300
What strategy would be best?
x = 3y + 4
5x + 2y = 12
Substitution because one of the equations is already solved for a variable
300
Solve the following System of Equations using whatever method
3x - y = 17
-x + y = -7
(5, -2)
400
How many solutions are there?
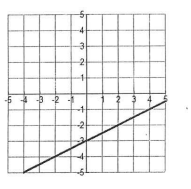
Infinitely Many Solutions
400
Solve the systems of equations:
-8x - 5y = -24
y = x + 10
(-2, 8)
400
Solve the systems of equations:
-7x - 10y = -17
6x + 7y = 13
(1,1)
400
What strategy would be best?
3x - 4y = 12
2x + 4y = 6
Elimination Method the coefficients on x are the same number with opposite signs
400
Solve the following System of Equations using whatever method
x = 3y - 5
2x - 3y = -4
(1, 2)
500
Solve the systems of linear equations by graphing:
500
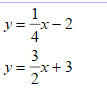
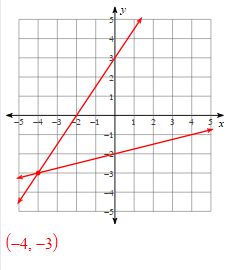
Solve the systems of equations:
y = 8x - 7
16x - 2y = 14
Infinitely Many Solutions
500
Solve the systems of equations:
3x + 4y = 11
2x + y = -1
(-3, -5)
500
What method would be the best?
y = 6 - 4x
4y = 3x + 8
Substitution because one equation has y isolated
500
The school that Stefan goes to is selling tickets to a choral performance. On the first day of ticket sales the school sold 3 senior citizen tickets and 1 child ticket for a total of $38. The school took in $52 on the second day by selling 3 senior citizen tickets and 2 child tickets. Find the price of a senior citizen ticket and the price of a child ticket.
Van: 18, Bus: 59