Systems with Graphs
Solving by Substitution
Solving by Elimination
Word Problems
Random
100
What is the solution?
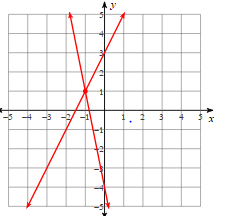
(-1,1)
100
Solve the systems of equations:
-3x + 4y = -2
y = -5
(-6, -5)
100
Solve the systems of equations:
14x + 2y = 26
-14x - 6y = -50
(1, 6)
100
What strategy would you use?
14x + 2y = 26
-14x - 6y = -50
elimination
100
Is the given point a solution to the system of equations?
Point: (-1,-3)
x + y = -4
3x - y = 0
Yes
200
How many solutions are there?
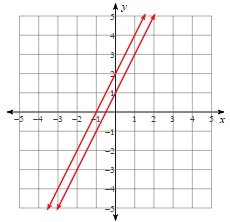
No Solutions
200
Solve the systems of equations:
-5x - 5y = 10
y = -4x -17
(-5, 3)
200
Solve the systems of equations:
-3x - 5y = 2
3x + 5y = 7
No Solution
200
Mrs. Morgan-Convery bought 2 new shirts and a dress for $45. She then went back and bought another shirt and 4 dresses for $70.
Write a systems of equations for the situation.
2x + y =45
x + 4y = 70
200
How many solutions to parallel lines have
none
300
Solve Using Graphing:
y = 5/3x + 2
y = -3
300
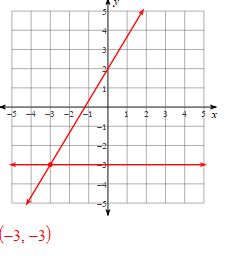
Solve the systems of equations:
y = -2x - 9
3x -6y = 9
(-3, -3)
300
Solve the systems of equations:
-6x - 10y = 4
6x + 10y = 0
No Solution
300
Mrs. Kessler went to Dunkin and bought one coffee and a bagel, her total was $7. Mrs. Manzo went to Dunkin and bought 2 coffees and 3 bagels and spent $18.
Write a systems of equations for this situation.
x + y = 7
2x + 3y = 18
300
What makes a system of equations have infinitely many solutions
They are the same line
400
How many solutions are there?
Infinitely Many Solutions
400
Solve the systems of equations:
-8x - 5y = -24
-x + y = 10
(-2, 8)
400
Solve the systems of equations:
-3x - 24y = -66
3x + 4y = -14
(-10, 4)
400
Mrs. Green rents 3 movies and 2 video games and spent a total of $25. Mrs. Hopler rents 2 movies and 1 video game and spends a total of $14.75. Set up a system of equations and solve
3x + 2y = 25
2x + y = 14.75
It costs $4.50 to rent one movie and $5.75 to rent one video game
400
To rent scooters, Sam’s Scooters charges a $30 fee plus $8 per hour. Rosie’s charges a $20 fee plus $10 per hour. Write equations for this system.
y= 8x + 30
y= 10x + 20
500
Solve the systems of linear equations by graphing:
500
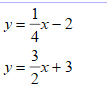
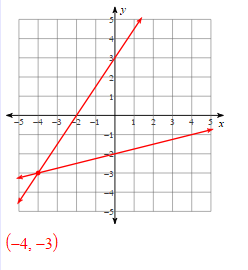
Solve the systems of equations:
-8x + y = -7
16x - 2y = 14
Infinitely Many Solutions
500
Solve the systems of equations:
-15x + 6y = -36
4x - 3y = 11
(2, -1)
500
At a carnival, 700 tickets were sold for a total amount of $5,500. An adult ticket cost $10 and a children’s ticket cost $5. Find the number of adult tickets and the number of children’s tickets sold. Set up a system of equations and solve
x + y =700
10x + 5y = 5500
400 adult tickets and 300 childrens tickets were sold
500
There are two numbers. The sum of the first number and twice the second number is 14. When the second number is subtracted from the first number, the result is 2. What are the two numbers?
6 and 4