x + 3y = 7
8x - 3y = 2
(1,2)
y = 2
x + 2y = 6
(2,2)
y = 2x + 2
y = x - 1
(3,-4)
What are 3 methods of solving systems of equations?
Graphing, Elimination, and Substitution
When graphing linear inequalities what does < and > mean?
Use a Dotted Line
4x - 3y = 16
5x + 3y = 20
(4,0)
y = 3x
2x + y = 10
(2,6)
y = 2x + 5
y = x + 3
(-2,1)
y = 2x + 3
y = 2x - 5
Lines with the same slope have:
No solution
What does ≤ and ≥ mean when graphing linear inequalities?
Use a solid Line
-2x - 9y = -25
-4x - 9y= 23
(-1,3)
y = 5x - 1
2y = 3x + 12
(2,9)
3x - 2y = 8
x + y = 6
(4,2)
How can you tell if a linear system has infinitely many solutions?
The equations are the same and the lines lie on top of each other
or
After solving you are left with a true statement such as 4=4
Systems of inequalities can only be solved by using ______
Graphing
4x - 9y = 2
12x - 5y = -38
(-4,-2)
2x - 3y = -2
y= -4x + 24
(5,4)
y = 1/2x + 2
y = 1/4x + 4
(8,6)
How many solutions does this system have:
y = -5x + 3
2y + 10x = 6
Infinitely Many Solutions
How is graphing systems of inequalities different than graphing systems of equations?
They use dotted lines sometimes and you have to shade to find the solution
The equations 5x + 2y = 48 and 3x + 2y = 32 represent the money collected from school concert tickets sales during two class periods. If x represents the cost for each adult ticket and y represents the cost for each student ticket, what is the cost for each adult ticket?
x=8
x + y = 10
-y = 5 + x
No solution
4x - 5y = 15
8x + 5y = 45
(5,1)
The method of solving equations where you add or subtract equations to end up with one variable.
Elimination
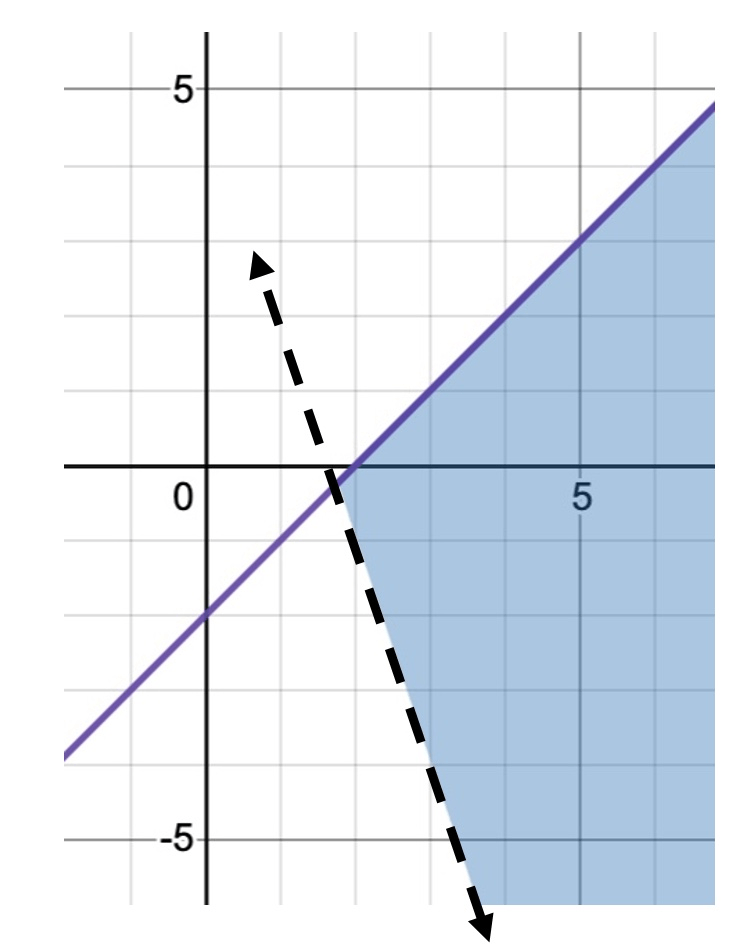
y ≤ x − 2
y > −3x + 5