Elimination
Substitution
Graphing
Mystery
Systems of Inequalities
100
x + 3 y = 5
2x - 3y = -8
(-1,2)
100
y = 2
3x + 2y = 10
(2,2)
100
y = 2x + 2
y = x - 1
(3,-4)
100
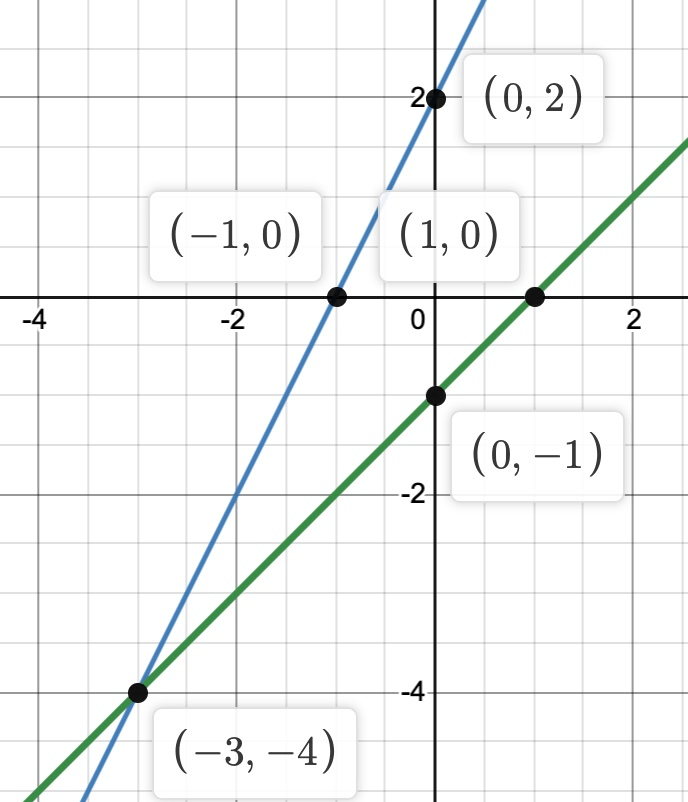
What are the 3 methods of solving systems of equations
graphing
elimination
substitution
100
When graphing linear inequalities what does < and > mean.
Dotted lines, solutions on the line may NOT be included.
200
4x - 3y = 16
5x + 3y = 20
(4,0)
200
y = x + 1
2x + y =10
(3,4)
200
y = 2x + 5
y = x + 3
(-2,1)
200
If Jane has 36 coins totaling $3.00, and the coins are all nickels and quarters, how many of each coin does she have?
Create a system. You do not need to solve.
x= nickels, y = quarters
x + y = 36
.05x + .25y = 3 or 5x + 25y = 300
200
Is (0,3) a solution to the graphed system of inequalities.
No
300
-2x - 9y = -25
-4x - 9y= 23
(-1,3)
300
y = 5x - 1
2y = 3x + 12
(2,9)
300
3x - 2y = 8
x + y = 6
(4,2)
300
The ninth graders are hosting the next school dance. They would like to make at least a $500 profit from selling tickets. The ninth graders estimate that at most 300 students will attend the dance. They will earn $3 for each ticket purchased in advance and $4 for each ticket purchased at the door. Write a system of inequalities. You do not need to solve.
x = the # of people who purchase tickets in advance y = the # of people who purchase at the door
3x + 4y ≥ 500
x + y ≤ 300
300
Which quadrant will the solutions to the system fall?
x > 5
y < -3
Quadrant 4
400
4x - 9y = 2
12x - 5y = -38
(-4,-2)
400
2x - 3y = -2
y= -4x + 24
(5,4)
400
y = 1/2x + 2
y = 1/4x + 4
(8,6)
400
You are running a concession stand at a basketball game. You are selling hot dogs and sodas. Each hot dog costs $1.50 and each soda costs $0.50. At the end of the night you made a total of $78.50. You sold a total of 87 hot dogs and sodas combined. You must report the number of hot dogs sold and the number of sodas sold. How many hot dogs were sold and how many sodas were sold?
x = the # of hot dogs sold, y = the # of sodas sold
1.50x + 0.50y = 78.50
x + y = 87
35 hot dogs, 52 sodas
400
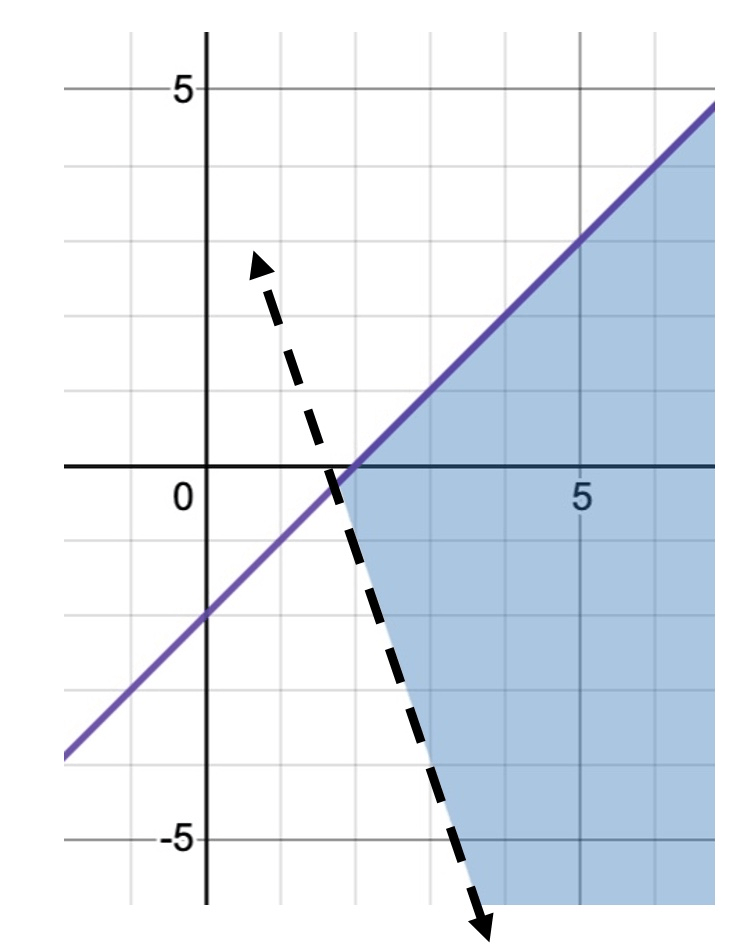
Solve the system by graphing.
y ≤ x − 2
y > −3x + 5
500
5x + 2y = 48
3x + 2y = 32
(8,4)
500
x + y = 10
-y = 5 + x
no solution
500
4x - 5y = 15
8x + 5y = 45
(5,1)
500
Mary babysits for $4 per hour. She also works as a tutor for $7 per hour. She is only allowed to work 13 hours per week. She wants to make at least $65. Write and graph a system of inequalities to represent this situation. Provide one ordered pair that satisfies the system. Explain what the ordered pair means.
x = babysitting, y = tutoring
x + y ≤ 13
4x + 7y ≥ 65
See graph
example: 2 hours babysitting and 9 hours tutoring
500
Solve the system by graphing:
8x - 4y > 24
-x + 12 ≤ 6y
See Answer Graph