elimination
substitution
graphing
vocabulary
mystery problems
100
x + 3 y = 5
2x - 3y = -8
(-1,2)
100
y = 2
3x + 2y = 10
(2,2)
100
y = 2x + 2
y = x - 1
(3,-4)
100
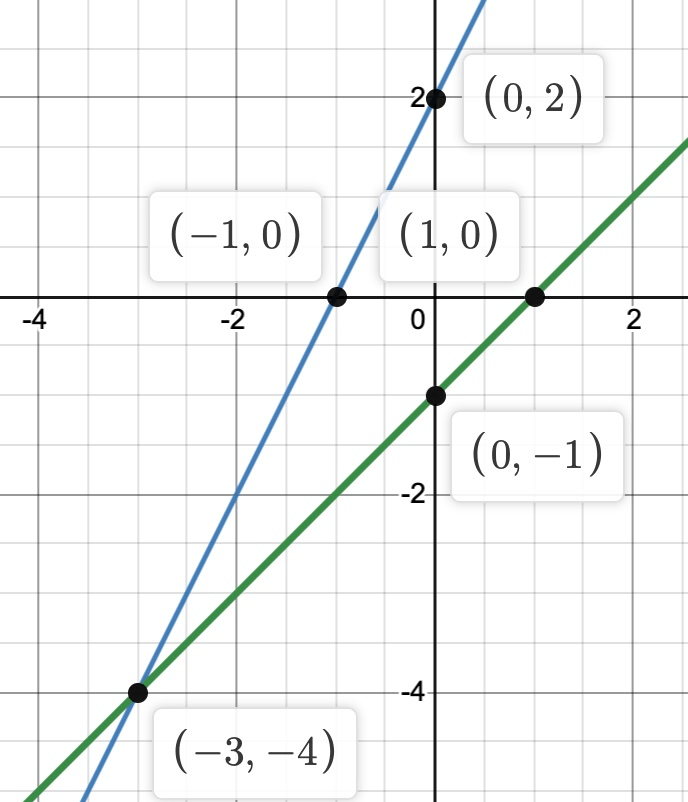
what are the 3 main methods of solving systems of equations
elimination
graphing
substitution
100
Choose a method and solve.
y = 1 and y = -7x - 6
(-1, 1)
200
4x - 3y = 16
5x + 3y = 20
(4,0)
200
y = x + 1
2x + y =10
(3,4)
200
y = 2x + 5
y = x + 3
(-2,1)
200
How can you tell that a system of equations has infinite solutions when looking at a graph
you will have the same line (one line on top of the other)
200
Chose a method and solve.
x + y = 10 and -x - y = -10
Infinite Solutions
300
-2x - 9y = -25
-4x - 9y= 23
(-1,3)
300
y = 5x - 1
2y = 3x + 12
(2,9)
300
3x - 2y = 8
x + y = 6
(4,2)
300
How can you tell if a linear system has infinitely many solutions when solving algebraically
when you end up with a true statement
300
Choose a method and solve.
4x + 5y = -22 and y = 3x + 7
(-3, -2)
400
4x - 9y = 2
12x - 5y = -38
(-4,-2)
400
2x - 3y = -2
y= -4x + 24
(5,4)
400
y = 1/2x + 2
y = 1/4x + 4
(8,6)
400
what does it mean about the solution when the lines are parallel on a graph
no solution
400
Choose a method and solve.
-4x + 10y = 26 and -2x + 2y = 4
(1, 3)
500
The equations 5x + 2y = 48 and 3x + 2y = 32 represent the money collected from school concert tickets sales during two class periods. If x represents the cost for each adult ticket and y represents the cost for each student ticket, what is the cost for each adult ticket?
$8.00
500
x + y = 10
-y = 5 + x
no solution
500
4x - 5y = 15
8x + 5y = 45
(5,1)
500
The method of solving equations where you add or subtract equations to end up with one variable.
elimination
500
The school that Beth goes to is selling tickets to a choral performance. On the first day of ticket sales the school sold 11 adult tickets and 13 student tickets for a total of $312. The school took in$195 on the second day by selling 3 adult tickets and 12 student tickets.
What is the price each of one adult ticket?
$13.00