Systems of Inequalities
Solving by Graphing
Solving by Elimination
Solving by Substitution
Word Problems
Mixture Problems
100
This method must be used to solve a system of inequalities
What is graphing
100
The quadrant in which the solution to the following system lies:
3x+y=6
x+3y=-6
What is Quadrant IV
100
The solution to the system of equations:
r + s = -6
r - s = -10
What is (-8, 2)?
100
The solution to the system:
x = 4y
2x + 3y = 22
What is (8, 2)
100
The sum of two numbers is 104. Their difference is 68. What are the numbers?
What are 86 and 18?
100
I have 19 coins in my pocket currently. When I go to use them, I have $2.75. If I only have quarters and nickels, How many of each are there?
9 Quarters and 10 nickels
200
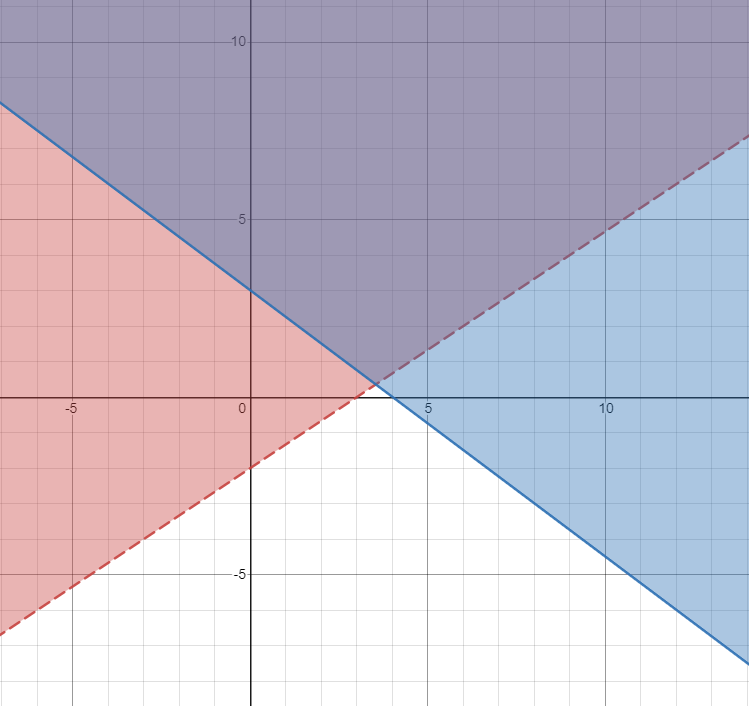
Graph the following inequalities
2x-3y<6
3x+4y>=12
200
The solution to the system of equations:
x+4y=-1
x=3
What is (3,-1)?
200
The solution to the system:
8a + 5b = 9
2a - 5b = -4
(1/2,1)
200
The solution to the system
y = x - 2
3x - y = 16
What is (7, 5)
200
A shopper bought 6 shirts and 8 hats for $700. A week later, at the same prices, he bought 9 shirts and 6 hats for $660. What was the cost of one shirt?
What is $30?
200
Leonidas paid a total of $2,780 for 261 tickets to the theater. Student tickets cost $10 and adult tickets cost $15. How many student tickets and how many adult tickets did he buy?
Leonidas bought 227 student tickets and 34 adult tickets
300
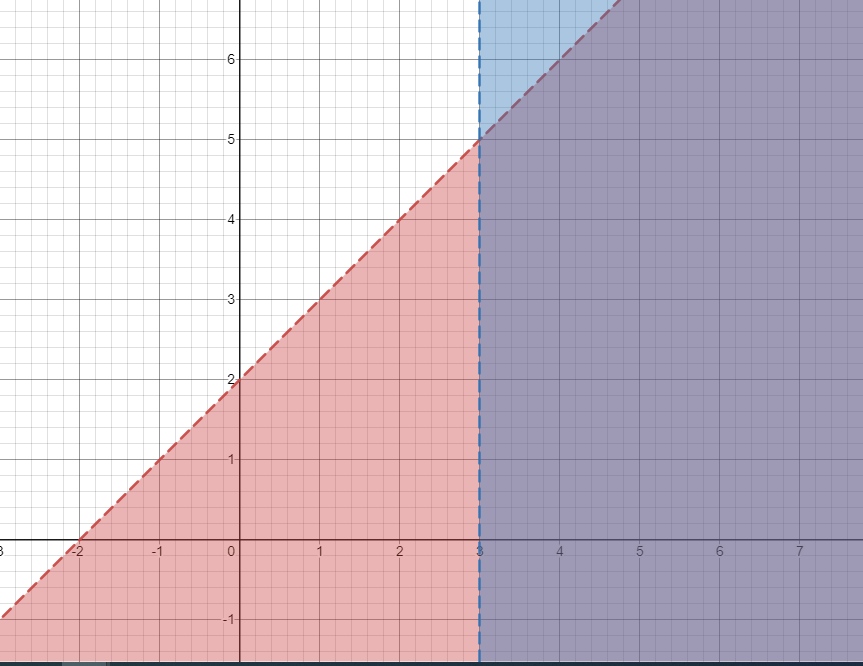
Show your solution to the system y < x + 2 and x > 3
300
The solution to the system of equations:
2x-y=5
4x-2y=10
Inf. Many solutions
300
The solution to the system:
2x + 3y = 6
3x + 5y = 15
What is (-15, 12)?
300
The solution to the system
y = 3x - 1
7x + 2y = 37
What is (3, 8)
300
The number of each type of ticket sold in the following situation: Tickets to a football game cost $5.oo if purchased before the day of the game. They cost $7.50 if purchased at the game. For a particular game, 600 tickets were sold and the receipts were $3500.
What is 400 advanced tickets, 200 game-day tickets?
300
Darth Vader's other daughter Ella wants to make 12 cups of party mix using candies and nuts. Her budget requires the party mix to cost her $1.29 per cup. The candies are $2.49 per cup and the nuts are $0.69 per cup. How many cups of candies and how many cups of nuts should she use?
Ella should use 4 cups of candies and 8 cups of nuts.
400
Graph the following inequalities
x+3y<5
y>=-1/3x+6
No Solution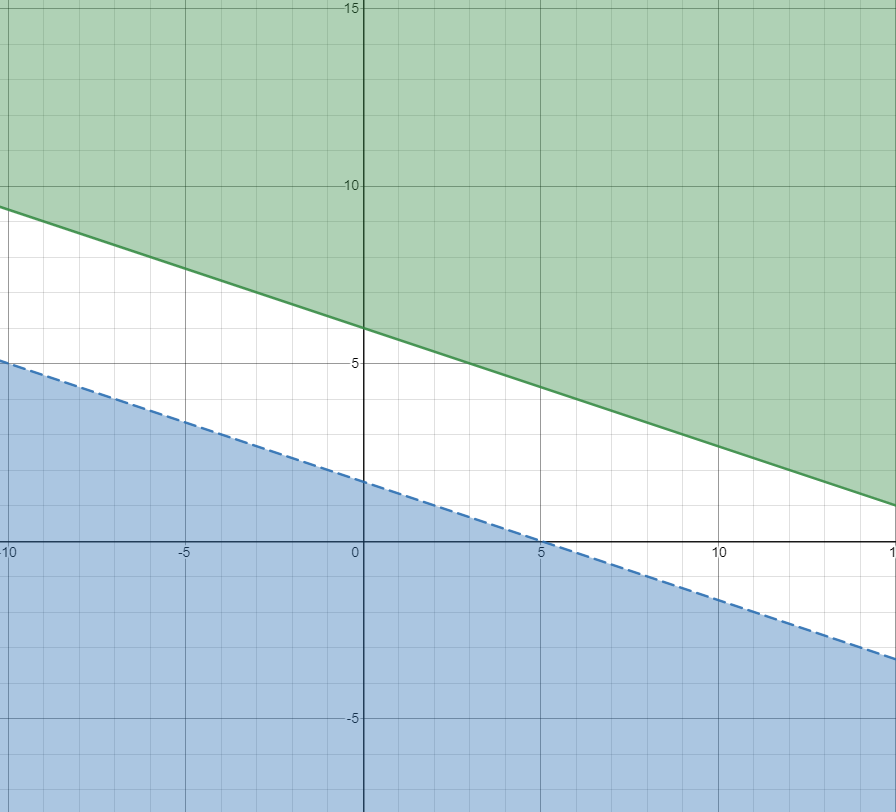
400
The solution to the system of equations
3x-3y=0
6x+15y=-42
What is (-2,-2)
400
The solution to the system
2a - 4b = 12
-8a + 16b = -48
What is infinitely many solutions?
400
The solution to the system
3s - 2t = 4
t = 2s - 1
What is (-2, -5)
400
Find the dimensions of a rectangle whose perimeter is 78 inches, when the length of the rectangle is twice its width
What is 26x13?
400
Marcus can drive his boat 36 miles down the river in three hours but takes four hours to return upstream. Find the rate of the boat in still water and the rate of the current.
The rate of the boat is 10.5 mph. The rate of the current is 1.5 mph.
500
How many points are in the answer to a system of linear inequalities where the shades intersect?
What is an infinite number of points.
500
The solution to the system of equations:
6y - 18x = 18
4y = 12x - 8
What is no solution
500
The solution to the system:
1/3x + 1/4y = 10
1/3x - 1/2y = 4
What is (24, 8)
500
The solution to the system
t + u = 12
t = 1/3u
What is (3, 9)?
500
The amount of money each child received when Mr. Hale left $25,000 divided between his son and daughter, with the son receiving $5000 less than the daughter.
What is $15,000 for the daughter and $10,000 for the son?
500
Bill Nye needs 70 liters of a 40% solution of acid. He has a 30% and a 60% solution available. How many liters of the 30% and how many liters of the 60% solutions should he mix to make the 40% solution?
Bill would need 70/3 liters of the 60% solution and 140/3 liters of the 30% solution.
Also will accept, 46.67 liters of 30% and 23.33 liters of 60%