Solutions
Solving Systems Algebraically
Solve by Graphing
Word Problems
100
Is the ordered pair (-1,2) a solution?
y = 3x + 5
3x+4y=5
YES
100
What is the solution of this systems of equations?
y=2x+5
y=3x+9
Solution: (-4,-3)
100
What is the solution of this systems of equations?
Solution = (2,2)
100
Celia has 30 coins that total $4.80. All of her coins are dimes, D, and quarters, Q. Which system of equations models this situation?
A) D+Q=4.80
.10D +.25Q =30
B) D+Q=30
.10D +.25Q =4.80
C) D+Q=30
.25D +.10Q =4.80
D) D+Q=4.80
.25D +.10Q =30
B) D+Q=30
.10D +.25Q =4.80
200
Is the ordered pair (5, -1) a solution?
x=-2y+3
y=x-4
NO
200
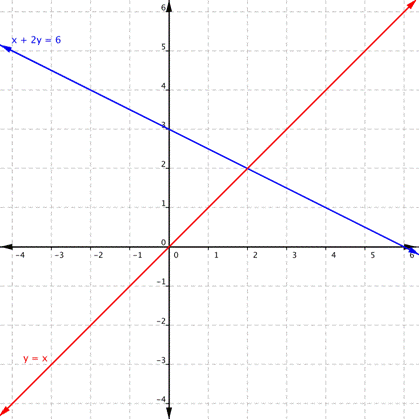
Solve the following system of equations ALGEBRAICALLY:
y=x+6
x+2y=6
Solution: (-2,4)
200
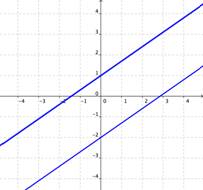
How many solutions does this systems of equations have?
NO SOLUTION
200
Mac joins a fitness club that has a membership fee of $20 plus $15 per month. Uri's club has a fee of $40 and charges $10 per month. Write a systems of equations to represent this situation. DO NOT SOLVE.
y=15x+20
y=10x+40
300
What is the value of x in the solution of the system of equations?
3x+ 2y = 12
5x -2y= 4?
2
300
Solve the following systems of equations ALGEBRAICALLY:
-7x-4y=-4
-9x-y=-30
Solution = (4,-6)
300
Graph the following systems of equations and identify the solution.
y=1/2x+1
y=-3/4x-4
Solution = (-4, -1)
300
Taxi company A charges $4 plus $0.50 per mile. Taxi company B charges $5 plus $0.25 per mile. Write a system of equations that could be used to represent this situation. After how many miles will the cost be the same for both taxi cabs?
y=.50x+4
y=0.25x+5
After 4 miles the cost will be the same.
400
If a+3b=13 and a+b=5 , what is the value of b?
b = 4
400
Solve the following systems of equations ALGEBRAICALLY:
3x+2y=4
4x+3y=7
Solution= (-2,5)
400
Graph the following systems of equations and identify the solution.
4x-2y=10
y=-2x-1
Solution = (1,-3)
400
Cass spent $14.85 to buy 13 flowers. She bought lilies, which cost $1.25 and tulips, which cost $0.90 each. How many of each flower did Cass buy?
9 lilies and 4 tulips
500
Find the value of k so that the system of equations below has no solution:
4x-8y=-4
kx-28y=-13
k = 14
500
Solve the following systems of equations ALGEBRAICALLY:
0.3x+0.2y=0.4
0.5x+0.4y=0.7
Solution =
(1, 1/2)
500
Graph the following systems of equations and identify the solution.
7x+y=-3
-14x-2y=6
Solution = Infinitely Many Solutions
500
The drama club is running a lemonade stand to raise money for its new production. A local grocery store donated cans of lemonade and bottles of water. Cans of lemonade sell for $2 each and bottles of water sell for $1.50 each. The club needs to raise $570 to cover the cost of renting costumes. The students will accept a total of 360 cans and bottles. Write a system of that can be used to represent this situation then solve it.
System:
2x + 1.5y = 570
x + y = 360
Solution: 60 cans of lemonade, 300 bottles of water