A
B
C
D
E
100
What is the solution?
(-1,1)
100
Solve the systems of equations using substitution:
-3x + 4y = -2
y = -5
(-6, -5)
100
Solve the systems of equations using Elimination:
14x + 2y = 26
-14x - 6y = -50
(1, 6)
100
What strategy would you use?
14x + 2y = 26
-14x - 6y = -50
elimination
100
Is the given point a solution to the system of equations?
Point: (2,6)
x + y = 8
3x - y = 0
Yes
200
How many solutions are there?
No Solutions
200
Solve the systems of equations using substitution:
-5x - 5y = 10
y = -4x -17
(-5, 3)
200
Solve the systems of equations using Elimination:
-3x - 5y = 2
3x + 5y = 7
No Solution
200
What strategy would you use?
-5x - 5y = 10
y = -4x -17
substitution
200
Is the given point a solution to the system of equations?
Point: (1/2, -2)
6x + 5y = -7
2x - 4y = -8
No
300
Solve Using Graphing:
y = 5/3x + 2
y = -3
300
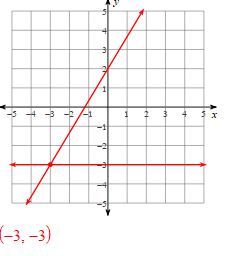
Solve the systems of equations using substitution:
y = -2x - 9
3x -6y = 9
(-3, -3)
300
Solve the systems of equations using Elimination:
-6x - 10y = 4
6x + 10y = 0
No Solution
300
Is there 1 solution, No solution, or Infinite solutions for the system of linear equations below?
3x - y = 19
-3x + y = 10
No Solutions
300
You are running a concession stand at a basketball game. You are selling hot dogs and sodas. Each hot dog costs $1.50 and each soda costs $0.50. At the end of the night you made a total of $78.50. You sold a total of 87 hot dogs and sodas combined. You must report the number of hot dogs sold and the number of sodas sold. How many hot dogs were sold and how many sodas were sold?
35 hotdogs, 52 sodas
400
How many solutions are there?
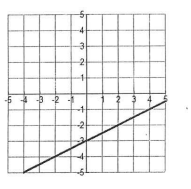
Infinitely Many Solutions
400
Solve the systems of equations using substitution:
-8x - 5y = -24
-x + y = 10
(-2, 8)
400
Solve the systems of equations using Elimination:
-3x - 24y = -66
3x + 4y = -14
(-10, 4)
400
The difference of two numbers is 3. Their sum is 13. Find the numbers.
5 and 8
400
Determine which method you would use to solve the following system of equations. Explain your reasoning.
0.3x - 0.2y = -2.1
0.6x + 1.3y = 0.9
Elimination - the equations are already in standard form.
500
Solve the systems of linear equations by graphing:
500
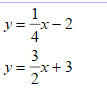
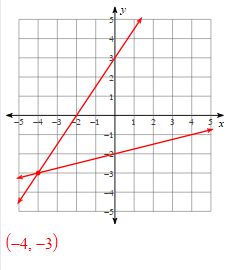
Solve the systems of equations using substitution:
-8x + y = -7
16x - 2y = 14
Infinitely Many Solutions
500
Solve the systems of equations using Elimination:
-15x + 6y = -36
8x - 6y = 22
(2, -1)
500
The school that Stefan goes to is selling tickets to a choral performance. On the first day of ticket sales the school sold 3 senior citizen tickets and 1 child ticket for a total of $38. The school took in $52 on the second day by selling 3 senior citizen tickets and 2 child tickets. Find the price of a senior citizen ticket and the price of a child ticket.
Senior Citizen: $8
Chid ticket: $14
500
Which method would you use to solve the system of equations? Explain your reasoning.
-6y + 2 = -4x
y - 2 = x
Substitution - the second equation is already solved for x.