How many Solutions?
Solve by Graphing
Solve by Substitution or Elimination
Real-World Application
100
Is there one solution, no solutions, or infinitely many solutions for the system of linear equations below?
One Solution (-4,-6)
100
What is the solution?
(-1,1)
100
Solve the systems of equations using Elimination:
14x + 2y = 26
-14x - 6y = -50
(1, 6)
100
Find the value of two numbers if their sum is 12 and their difference is 4
4 and 8
200
Is there one solution, no solution, or infinitely many solutions for the system of linear equations below?
y = 3x - 5
y = 3x + 7
No Solution
200
How many solutions are there?
No Solutions
200
Solve the systems of equations using substitution:
-5x - 5y = 10
y = -4x -17
(-5, 3)
200
The sum of two numbers is 30 and their difference is 12. Find the two numbers.
(21, 9)
300
Is there one solution, no solution, or infinitely many solutions for the system of linear equations below?
y = (-5/3)x + 3
y = (1/3)x - 3
One Solution
300
Solve Using Graphing:
y = 5/3x + 2
y = -3
300
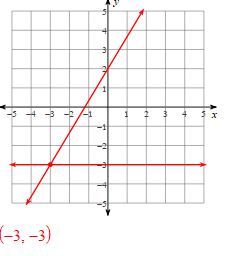
Solve the systems of equations using substitution:
y = -2x - 9
3x -6y = 9
(-3, -3)
300
The school that Stefan goes to is selling tickets to a choral performance. On the first day of ticket sales the school sold 3 senior citizen tickets and 1 child ticket for a total of $38. The school took in $52 on the second day by selling 3 senior citizen tickets and 2 child tickets. Find the price of a senior citizen ticket and the price of a child ticket.
senior citizen ticket: $8, child ticket: $14
400
Is there one solution, no solution, or infinitely many solutions for the system of linear equations below?
y = 3x + 9
4x - 2y = 18
One Solution
400
How many solutions are there?
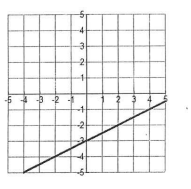
Infinitely Many Solutions
400
Solve the systems of equations using Elimination:
-x - 8y = -22
3x + 4y = -14
(-10, 4)
400
Mrs. Wilson tells you that the next test is worth 100 points and contains 38 problems. Multiple-choice questions are worth 3 points and word problems are worth 4 points. How many of each type of questions are in there?
(30,8)
8 word problems
30 Multiple Choice
500
Is there one solution, no solution, or infinitely many solutions for the system of linear equations below?
18x - 4y = 12
-9x + 2y = -6
Infinitely Many Solutions
500
Solve the systems of linear equations by graphing:
500
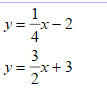
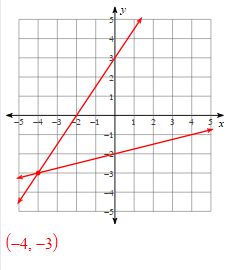
Solve the systems of equations using Elimination:
-5x + 2y = -12
4x - 3y = 11
(2, -1)
500
Adult tickets for the school musical sold for $3.50 and student tickets sold for $2.50. On a given night, 321 tickets were sold for $937.50. How many of each kind of ticket were sold?
(135, 186)
adults-135
Children- 186