Methods & Solutions
Graphing
Substitution
Definitions
100
What are the two methods for solving systems of equations that we've learned so far?
Graphing Method, Substitution Method,
100
When graphing a system of equations, the solution lies at the point of ______________?
"intersection"
100
You solved a system of equations using substitution and you ended up with
0x=-7
How many solutions does the system have?
No solution
100
The answer of a systems of linear equations.
the solution
200
Is the ordered pair (- 2, 8) a solution of
8x + 2y = 0
x - 2y = -18
YES
200
What is the solution of this systems of equations?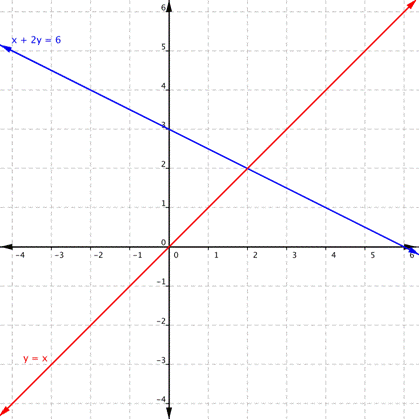
(2,2)
200
You solved a system of equations using substitution and you ended up with
0x=0
How many solutions does the system have?
infinitely many solutions
200
The two lines have the same slope and different y-intercept. The number of solutions for this type of systems of equations is:
none
300
In what method would you isolate one variable to solve?
Substitution
300
If two lines have "no solution" in a system of equations, what is true about their slopes?
What is "they are the same?"
300
The solution of the following system of equations:
x + 2y = 13
-2x - 3y = -18
(-3, 8)
300
How is the solution to a system of equation written?
an ordered pair
(x,y)
400
What would you substitute into the second equation to solve this system?
y = -2x + 3
4x + 2y = 6
-2x + 3
400
What does a system of linear equations with infinitely many solutions look like when graphed?
What is one line?
400
Solve the following system of equations using substitution.
y=x+6
x+2y=6
(-2, 4)
400
The lines have the same slope and same y-intercept. What is the number of solutions for this type of system of equations?
many
500
Is the ordered pair (-1,2) a solution of
x - y=-3
2x+y=0?
YES
500
What is the solution to this system of equations?
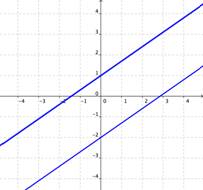
NO SOLUTION
500
The solution of the following system of equations:
y=-3x
-3x+3y=0
What is "(0,0)"?
500
What is the 3rd method for solving systems of equations that we have not learned yet?
elimination