What is the solution?

(-1,1)
Solve the systems of equations using substitution:
y=3x-10
x=2
(2,-4)
Solve the systems of equations using Elimination:
-x - 5y = 4
x + 7y = -8
(6, -2)
How many solutions would a system of linear equations have if the equations are parallel and different y-intercepts?
Zero Solutions
You are at the beach with your group of friends, and it’s your turn to buy the snacks. You go up to the concession stand to buy 5 ice cream cones and 6 fruit smoothies totaling $65. You forget 2 ice cream cones, so you go back up to the stand to purchase them (with everything the same price) totaling $14. What are the two equations?
2x = 14
How many solutions are there?

No Solutions
Solve the systems of equations using substitution:
y=2x-10
y=4x+8
(-9,-28)
Solve the systems of equations using Elimination:
2x - 3y = 9
-2x + y = -2
(-1, -4)
How many solutions would a system of linear equations have if the equations are parallel and have the same y-intercept?
Infinite Solutions
A group of tourists spends $594 to rent tents and grills for their weekend camping. They rent a total of 5 tents and 7 grills. The cost of renting a tent is 4 times as much as renting the grills. How much does it cost to rent one tent?
Solve Using Graphing:
y = 5/3x + 2
y = -3
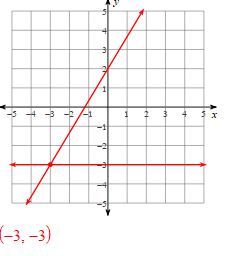
Solve the systems of equations using substitution:
y = -2x - 9
3x -6y = 9
(-3, -3)
Solve the systems of equations using Elimination:
-6x - 10y = 4
6x + 10y = 0
No Solution
Is there 1 solution, No solution, or Infinite solutions for the following question?
3x - y = 19
-3x + y = 10
No Solutions
Person A buys 17 water bottles and 6 personal pizzas for $166. Person B buys 11 water bottles and 3 personal pizzas for $88. Find the cost of each item.
Personal pizzas cost $22
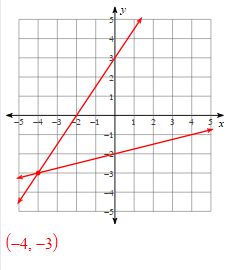
Solve this by graphing:
y = 2x - 4
y = -1/3 x + 3
(3,2)
Solve the systems of equations using substitution:
2x - y = 6
x = y + 5
Solve the systems of equations using Elimination:
-3x - 24y = -66
3x + 4y = -14
(-10, 4)
How many solutions does the system have?
3y + 4x = 6
12y + 16x = 24
These are the same exact line, therefore they have
Infinite Solutions
A group of tourists spends $168 to rent snorkels and fins. A total of 10 snorkels and 12 pairs of fins are rented. Renting a snorkel costs three times as much as renting a pair of fins. How much does it cost to rent a snorkel?
$12
Solve the systems of linear equations by graphing:
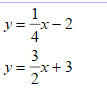
Solve the systems of equations using substitution:
-8x + y = -7
16x - 2y = 14
Infinitely Many Solutions
Solve the systems of equations using Elimination:
-15x + 6y = -36
-8x + 6y = -22
(2, -1)
How many solutions does the system have?
-6y + 2 = -4x
y - 2 = x
Different slopes
One solution
y=2/3x+1/3
y=x+2