Systems Trivia
Solve by Graphing
Solve by Substitution
Number of Solutions
Word Problems
100
In the form y = mx + b
What do m and b represent?
m = slope
b = y-intercept
100
What is the solution?
(-1,1)
100
Solve the systems of equations using substitution:
y=3x-10
x=2
(2,-4)
100
How many solutions would a system of linear equations have if the equations are parallel and different y-intercepts?
Zero Solutions
100
The owner of a table is ordering tables and chairs. He wants to have only tables for 2 and tables for 4. The total number of people that can be seated in the restaurant is 120.
Name three combinations of 2-seat tables and 4-seat tables that will seat 120.
(2-seaters are x and 4-seaters are y)
(60,0)
(58,1)
(56,2)
(54, 3) etc
200
What is the slope of this equation?
1/2
200
How many solutions are there?
No Solutions
200
Solve the systems of equations using substitution:
y=2x-10
y=4x+8
(-9,-28)
200
How many solutions would a system of linear equations have if the equations are parallel and have the same y-intercept?
Infinite Solutions
200
Diego has $11 and has been saving $5 a week to get a new phone. Lin has $60 and has been spending 2 each week to buy art supplies. Is there a week when they will have the same amount of money? How much?
They will both have $46 at week 7.
300
What is the y-intercept of this equation? Write as a coordinate pair.
(0,-2)
300
Solve Using Graphing:
y = 5/3x + 2
y = -3
300
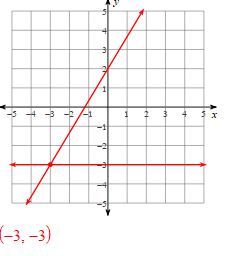
Solve the systems of equations using substitution:
y = -2x - 9
3x -6y = 9
(-3, -3)
300
Is there 1 solution, No solution, or Infinite solutions for the following question?
y = 3x + 19
y = 3x + 10
No Solutions
300
A farm has chickens and cows. All chickens have 2 legs and all cows have 4 legs. Altogether there are 82 animal legs on the farm. Complete the table with possible combinations of chicken and cows.
400
How do you use the y-intercept and slope when graphing?
Something like:
400
Solve this by graphing:
y = 2x - 4
y = -1/3 x + 3
(3,2)
400
Solve the systems of equations using substitution:
2x - y = 6
x = y + 5
(1, -4)
400
How many solutions does the system have?
y = -4x + 24
y = -4(x - 6)
These are the same exact line, therefore they have
Infinite Solutions
400
If the farm has 30 total animals and 82 animal legs, then how many chickens and cows could there be? Here is a graph that shows possible combinations of cows and chickens that add up to 30 (on paper)
19 chickens and 11 cows
500
Graph the following line:
500
Solve the systems of linear equations by graphing:
500
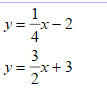
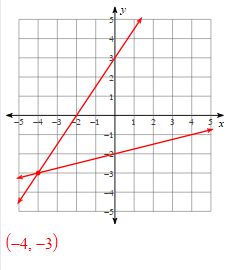
Solve the systems of equations using substitution:
-8x + y = -7
y = 8x - 7
Infinitely Many Solutions
500
How many solutions does the system have?
y = -x - 2
y = x + 2
Different slopes
One solution
500
Clare and Noah play a game in which they earn the same number of points for a goal and lose the same number of points for a penalty. Clare makes 6 goals and 3 penalties, ending the game with 6 points. Noah earns 8 goals and 9 penalties and ends the game with -22 points. How much are each point and penalty worth?
Points are worth 4. Penalties are worth -6