Solve by Graphing
Solve by Substitution
Solve by Elimination
Writing Systems
100
MYSTERY QUESTION** DOUBLE POINTS
WHAT IS Ms. Fouchie's FAVORITE COLOR?
Green
100
Solve the systems of equations using substitution:
–3x − 6y = –9
x = 7
(7,-2)
100
Solve the systems of equations using Elimination:
-3x - 24y = -66
3x + 4y = -14
(-10, 4)
100
Two families went to Rollercoaster World. The Brown family paid $170 for 3 children and 2 adults. The Peckham family paid $360 for 4 children and 6 adults. If x is the price of a child's ticket in dollars and y is the price of an adult's ticket in dollars, write a system of equations that models this situation.
3x + 2y = 170
4x + 6y = 360
200
What is the solution?
(-1,1)
200
Solve the systems of equations using substitution:
-3x + 4y = -2
y = -5
(-6, -5)
200
Solve the systems of equations using Elimination:
14x + 2y = 26
-14x - 6y = -50
(1, 6)
200
At an amusement park, the cost for an adult admission is a, and for a child the cost is c. For a group of six that included two children, the cost was $325.94. For a group of five that included three children, the cost was $256.95. All ticket prices include tax. Write a system of equations, in terms of a and c, that models this situation.
2c + 4a = 325.94
3c + 2a = 256.95
300
How many solutions are there?
No Solutions
300
Solve the systems of equations using substitution:
x = –1
x − 2y = –15
(-1, 7)
300
Solve the systems of equations using Elimination:
-3x - 5y = 2
3x + 5y = 7
No Solution
300
An ice cream shop sells small and large sundaes. One day, 30 small sundaes and 50 large sundaes were sold for $420. Another day, 15 small sundaes and 35 large sundaes were sold for $270. Sales tax is included in all prices. If x is the cost of a small sundae and y is the cost of a large sundae, write a system of equations to represent this situation.
30x + 50y = 420
15x + 35y = 270
400
Write the equations for the system below:
y = 5/3x + 2
y = -3
400
Solve the systems of equations using substitution:
x = –8
–x − 3y = –4
(-8, 4)
400
Solve the systems of equations using Elimination:
-6x - 10y = 4
6x + 10y = 0
No Solution
400
Dana went shopping for plants to put in her garden. She bought three roses and two daisies for $31.88. Later that day, she went back and bought two roses and one daisy for $18.92. If r represents the cost of one rose and d represents the cost of one daisy, write a system of equations that models this situation.
3r + 2d = 31.88
2r + d = 18.92
500
Solve the systems of linear equations by graphing:
500
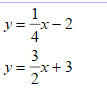
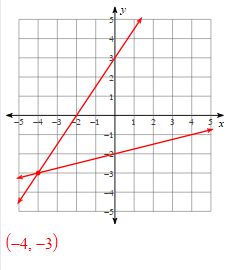
–7x − 2y = 11
x = 1
(1,-9)
500
Solve the systems of equations using Elimination:
–x + 6y = 14
3x − 6y = –18
(-2, 2)
500
At a local garden shop, the price of plants includes sales tax. The cost of 4 large plants and 8 medium plants is $40. The cost of 5 large plants and 2 medium plants is $28. If x is the cost of a large plant and y is the cost of a medium plant, write a system of equations that models this situation.
4x + 8y = 40