Solve by Graphing
Solve by Substitution
Solve by Elimination
Checking Solutions & Word Problems
Systems Trivia
100
What is the solution?
(-1,1)
100
Solve the systems of equations using substitution:
y=3x-10
x=2
(2,-4)
100
Solve the systems of equations using Elimination:
-x - 5y = 4
x + 7y = -8
(6, -2)
100
Tell whether the ordered pair is a solution of the system of linear equations.
(2,5)
x+y=7
2x-3y=-11
(2,5) is a solution to the system
100
What is the slope of this equation?
y = -1/2 x +7
-1/2
200
How many solutions are there?
No Solutions
200
Solve the systems of equations using substitution:
y=2x-10
y=4x+8
(-9,-28)
200
Solve the systems of equations using Elimination:
2x - 3y = 10
-2x + y = -2
(-1, -4)
200
Tell whether the ordered pair is a solution of the system of linear equations.
(1,-2)
2x+y=0
-x+2y=5
(1,-2) is NOT a solution to the system
200
In the form y = mx + b
What do m and b represent?
m = slope
b = y-intercept
300
Solve Using Graphing:
y = 5/3x + 2
y = -3
300
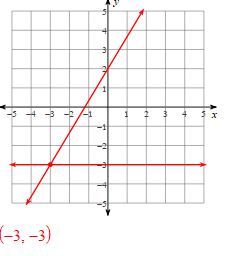
Solve the systems of equations using substitution:
y = -2x - 9
3x -6y = 9
(-3, -3)
300
Solve the systems of equations using Elimination:
-6x - 10y = 4
6x + 10y = 0
No Solution
300
You plant a spruce tree that grows 4 inches per year and a hemlock tree that grows 6 inches per year. Initially, the spruce tree was 14 inches and the hemlock tree was 8 inches. When will the trees be the same heights?
a. Define the variables.
b. Write the system of equations.
a. h - height of trees, t - time
b. h=4t+14
h=6t+8
300
What is the y-intercept of this equation?
y = 6x +5
(0,5)
400
Solve this by graphing:
y = 2x - 4
y = -1/3 x + 3
(3,2)
400
Solve the systems of equations using substitution:
2x - y = 6
x = y + 5
(1, -4)
400
Solve the systems of equations using Elimination:
-3x - 24y = -66
3x + 4y = -14
(-10, 4)
400
Two students are going to the store to buy school supplies for the new school year. One of the students buys 2 packs of pencils and 3 packs of pens for $8.25. Her friend purchases 5 packs of pencils and 2 packs of pens for $11.00. Define the variables and write the system of equations to determine the price of pencils and pens.
x - price of a pack of pencils
y - price of a pack of pens
2x+3y=8.25
5x+2y=11.00
400
What is true of lines with no solution?
They are parallel
500
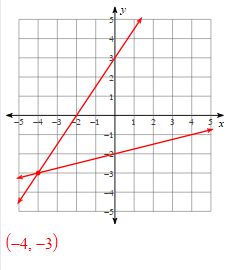
Solve the systems of linear equations by graphing:
500
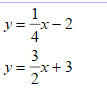
Solve the systems of equations using substitution:
-8x + y = -7
16x - 2y = 14
Infinitely Many Solutions
500
Solve the systems of equations using Elimination:
-15x + 6y = -36
-8x + 6y = -22
(2, -1)
500
In a football game, all of the home team's points are from 7-point touchdowns and 3-point field goals. The team scores six times for a total of 26 points. Define the variables and write a system of linear equations to find the number of touchdowns and field goals that the home team scores.
t - touch downs
f - field goals
7t+3f=26
t+f=6
500
What does it mean if a system of equations has infinite solutions?
They are the same line