What is the solution?
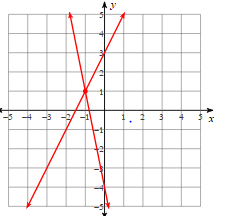
(-1,1)
Solve the systems of equations using substitution:
-3x + 4y = -2
y = -5
(-6, -5)
Solve the systems of equations using Elimination:
14x + 2y = 26
-14x - 6y = -50
(1, 6)
How many solutions would the following system of equations have?
y = 3x - 2
y = 3x - 4
They have the same slope and different y-intercepts so they will never meet. NO SOLUTION!
Two numbers have a sum of 117. The larger number is 42 less than twice the smaller number.
Write a system of equations that can help you solve this problem?
x+y=117
y=2x-42
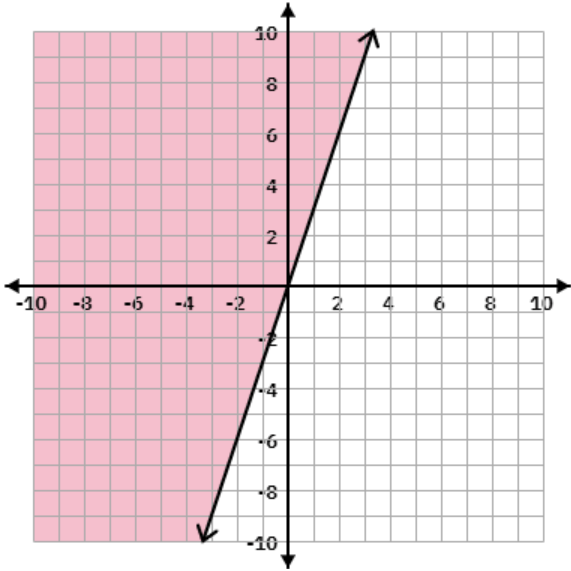
Graph the following on your whiteboard.
y>= -3x
Does your graph start at y=0, have a solid line, a slope of -3/1 and shaded above the y-intercept?
How many solutions are there?
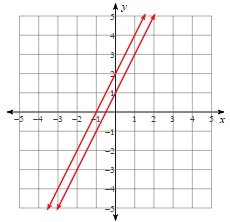
No Solutions
Solve the systems of equations using substitution:
-5x - 5y = 10
y = -4x -17
(-5, 3)
Solve the systems of equations using Elimination:
x+3y=7
2x+2y=6
(1,2)
How many solutions would the following system of equations have?
y = 3x - 2
y = -2x -2
The slopes are different so this will meet at one point.
Two pizzas and four nachos cost $62. Four pizzas and ten nachos cost $140. How much does each pizza and sandwich cost? Set up the equations for the system of equations. Do not solve.
2x + 4y = 62
4x + 10y = 140
Which of the following are solutions to the system of equations?
(2,4), (0,0), (6,6), (0,4), (4,6)
(0,4)
Solve Using Graphing:
y = 5/3x + 2
y = -3
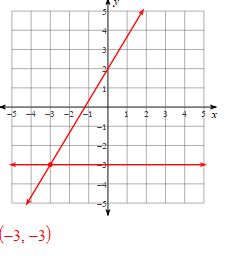
Solve the systems of equations using substitution:
y = -2x - 9
3x -6y = 9
(-3, -3)
Solve the systems of equations using Elimination:
-6x - 10y = 4
6x + 10y = 0
No Solution
How many solutions does this system of equations have?
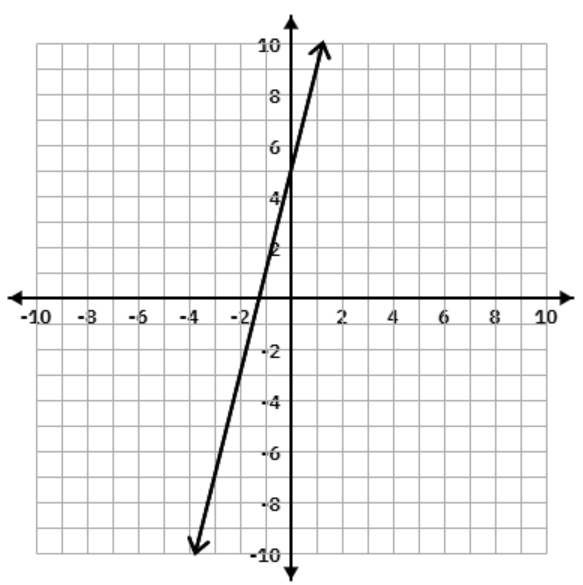
Infinite
Sam and Henry each opened a savings account on the same day. Sam started by putting $817 in his account, and he will deposit an additional $372 each week. Henry made an initial deposit of $987, and he will add $355 more each week. Set up the system of equations but do not solve for the number of weeks it would take to earn the same amount.
x = weeks y=amount saved
y=372x+817
y=355x+987
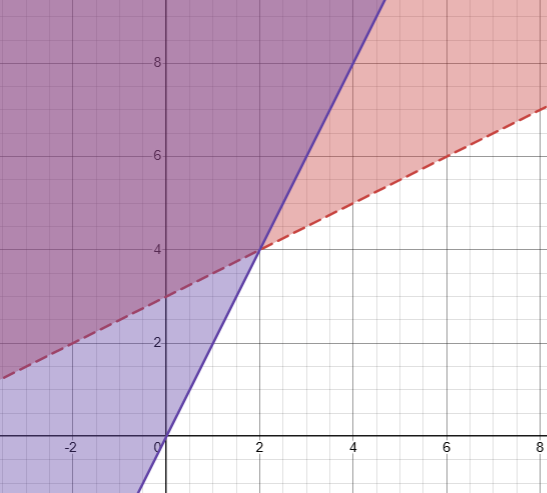
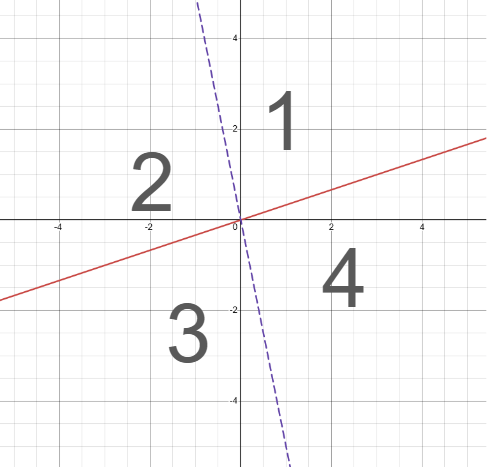
Which area represents that solution to the system of inequalities?
y\le\frac{1}{3}x and y<-5x
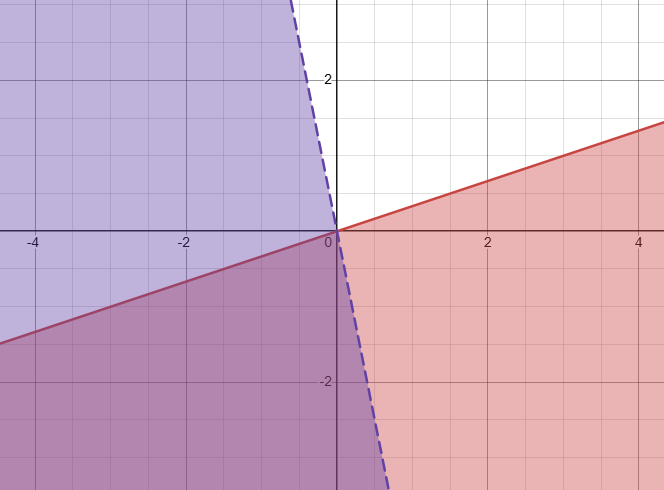
Part 3
How many solutions are there to this system of equations?
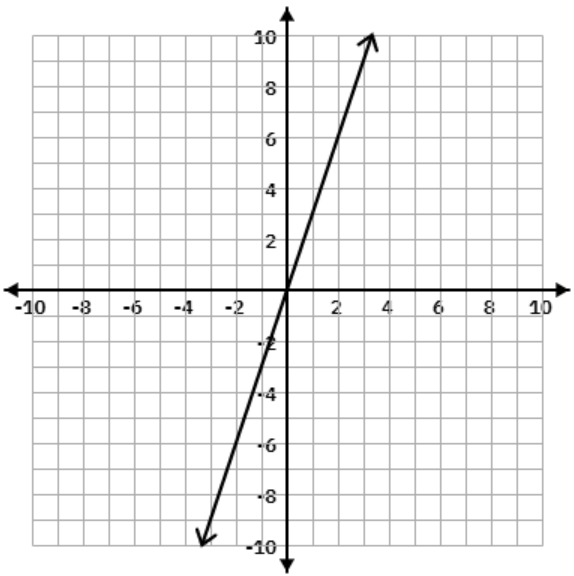
Infinitely Many Solutions
Solve the systems of equations using substitution:
-8x - 5y = -24
-x + y = 10
(-2, 8)
Solve the systems of equations using Elimination:
8x - 2y = -8
5x - 4y = 17
(-3,-8)
Is the given point a solution to the system of equations?
(1/2, -2)
6x + 5y = -7
2x - 4y = -8
No
Plug in 1/2 for x and -2 for y into both equations. It must be true for both.
Rich has $8.10 in his piggy bank which consists of 82 coins that are nickels and quarters. How many of each coin does Rich have? Show how to set up the system of equations.
x = nickels and y=quarters
0.05x + 0.25y = 8.10
x + y = 82
Which area represents that solution to the system of inequalities?
y<4x+4 and y<4x
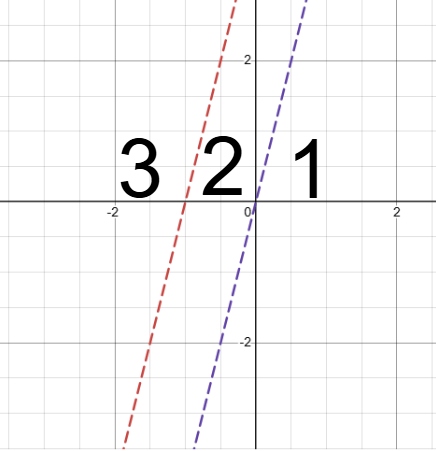
Section 1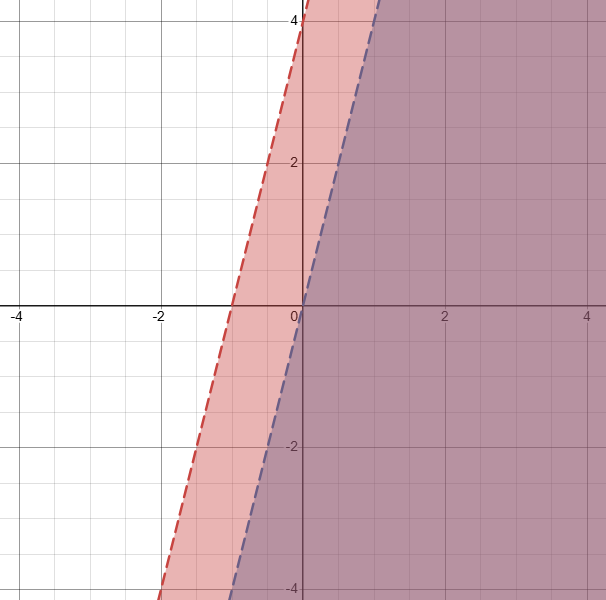
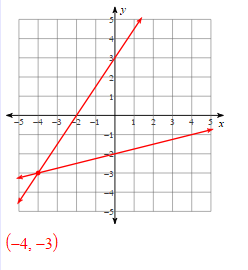
Solve the systems of linear equations by graphing:
y=1/4x-2
y=3/2x+3
Solve the systems of equations using substitution:
-8x + y = -7
16x - 2y = 14
Infinitely Many Solutions
Solve the systems of equations using Elimination:
4x + 3y = -9
3x + 2y = -11
(-15,17)
How many solutions does the following system have?
3x - 2y = 38
x = 6 - y
one solution
They meet at (10,-4)
Paul is designing a rectangular garden. The length of his garden is 10 feet less than three times its width. If the perimeter is 90, what are the dimensions of the garden? Set up but do not solve the equations.
x=length and y=width
2x + 2y = 90
x = 3y - 10
Solved (30,15)
Graph the following on your whiteboard.
2x-5y<10
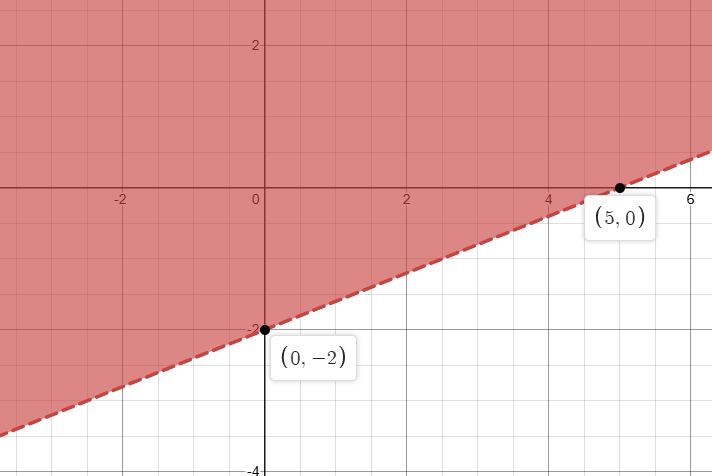 Standard form allows you to find the x and y-intercepts easily. Then test a point to see if it is true.
Standard form allows you to find the x and y-intercepts easily. Then test a point to see if it is true.