Solve by Graphing
Solve by Substitution
Solve by Elimination
Definitions
Word Problems
100
What is the solution?
(-1,1)
100
Solve the systems of equations using substitution:
-3x + 4y = -2
y = -5
(-6, -5)
100
Solve the systems of equations using Elimination:
14x + 2y = 26
-14x - 6y = -50
(1, 6)
100
In the equation y =mx+b, what letter represents the slope?
What is B?
100
Find the value of two numbers if their sum is 9 and their difference is 3
(6, 3)
x = 6
y = 3
200
How many solutions are there?
No Solutions
200
Solve the systems of equations using substitution:
-5x - 5y = 10
y = -4x -17
(-5, 3)
200
Solve the systems of equations using Elimination:
-3x - 5y = 2
3x + 5y = 7
No Solution
200
What's a coefficient?
A number in front of a variable
200
The difference of two numbers is 5 and the sum of those same two numbers is 9. What are the two numbers?
(7,2)
x = 7
y = 2
300
Solve Using Graphing:
y = 5/3x + 2
y = -3
300
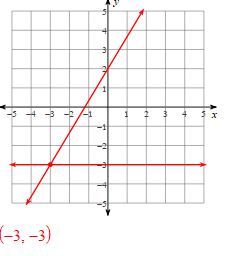
Solve the systems of equations using substitution:
y = -2x - 9
3x -6y = 9
(-3, -3)
300
Solve the systems of equations using Elimination:
-6x - 10y = 4
6x + 10y = 0
No Solution
300
Explain what solving through graphing means
Graphing two lines to find an intersection point, thus solving the system
300
Catalina is hosting a movie night for two days with a discount for seniors and children. On the first day they made $28 from selling 4 children's tickets and 2 senior's tickets. On the second day they made $44 from selling 4 children's tickets and 6 senior's tickets. What is the cost of an individual senior's ticket and what is the cost of an individual children's ticket?
(5, 4)
C = 5
S = 4
400
How many solutions are there?
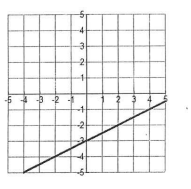
Infinitely Many Solutions
400
Solve the systems of equations using substitution:
-8x - 5y = -24
-x + y = 10
(-2, 8)
400
Solve the systems of equations using Elimination:
-3x - 24y = -66
3x + 4y = -14
(-10, 4)
400
The following equation, 3x + 7y = 12 is an example of a _____ equation
What is linear?
400
Matt and Ming are selling fruit for a school fundraiser. Customers can buy small boxes of oranges and large boxes of oranges. Matt sold 3 small boxes of oranges and 14 large boxes of oranges for a total of $203. Ming sold 11 small boxes of oranges and 11 large boxes of oranges for a total of $220. Find the cost each of one small box of oranges and one large box of oranges.
small box of oranges: $7
large box of oranges: $13
500
Solve the systems of linear equations by graphing:
500
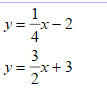
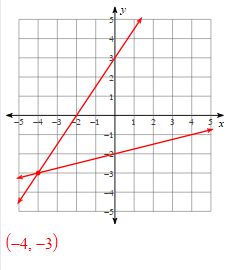
Solve the systems of equations using substitution:
-8x + y = -7
16x - 2y = 14
Infinitely Many Solutions
500
Solve the systems of equations using Elimination:
-15x + 6y = -36
8x - 6y = 22
(2, -1)
500
Explain the elimination method
Adding or subtracting equations together that have a variable with the same coefficient in order to eliminate the variable
500
The school that Stefan goes to is selling tickets to a choral performance. On the first day of ticket sales the school sold 3 senior citizen tickets and 1 child ticket for a total of $38. The school took in $52 on the second day by selling 3 senior citizen tickets and 2 child tickets. Find the price of a senior citizen ticket and the price of a child ticket.
senior citizen ticket: $8
child ticket: $14