Graphs of Systems of Equations
Substitution Method
Elimination Method
Systems of Inequalities
Miscellaneous
100
Describe which set of lines have no solution in the graph below.
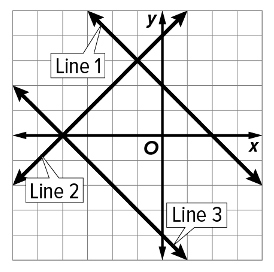
Line 1 and Line 3 are parallel lines so that means they never intersect, therefore there is no solution to the system of Line 1 and Line 3.
100
Solve by using substitution.
{(3x-y=-7),(y=4x+11):}
(-4, -5)
100
Use elimination to solve the system of equations.
{(3x+5y=11),(5x-5y=5):}
(2,1)
100
Write the system of inequalities for the graph below.
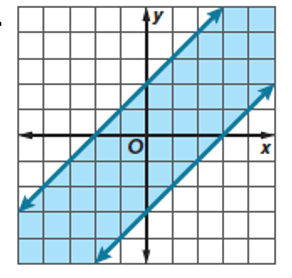
{(y<=x+2),(y>=x-3):}
100
Solve.
2(sqrt9+sqrt16)
14
200
Describe which system of equations would have one solution at the point (-4, 0).
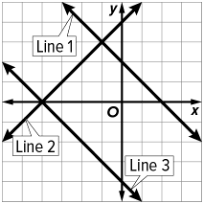
The system that consists of Line 2 and Line 3 have a solution at the point (-4, 0).
200
Use substitution to solve the system of equations.
{(5x-3y=-25),(x+4y=18):}
(-2, 5)
200
Use elimination to solve the system of equations.
{(5x+13y=20),(-5x-3y=30):}
(-9, 5)
200
Write a system of inequalities for the graph below.
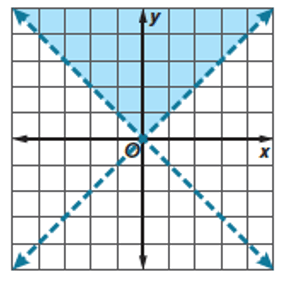
{(y>x),(y>--x):}
200
Determine the number of solutions in the equation below.
3(2x-4)-6=6(x-3)
Infinitely many solutions.
300
Determine whether the system of equations is consistent or inconsistent and if it is independent or dependent.
{(3x+y=-5),(9x+3y=-15):}
Consistent dependent since they are both the same equations.
300
Use substitution to solve the system of equations.
{(5x+3y=5),(x+2y=-13):}
(7,-10)
300
Use elimination to solve the system of equations.
{(3x+6y=30),(5x+6y=6):}
(-12,11)
300
Draw an example of a system of inequalities that are parallel lines but do have a solution set.
300
Write the equation of the line that is passes through the point (1,2) with a slope of -3
y=-3x+5
400
The number of items sold at Store 1 can be represented by
y = 200x + 300, where x represents the number of days and y represents the number of items sold. The number of items sold at Store 2 can be represented by y = 200x + 100, where x represents the number of days and y represents the number of items sold. Look at the graph of the system of equations and determine whether it has no solution, one solution, or infinitely many solutions.
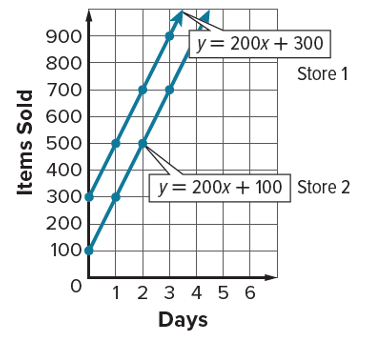
No solution
400
Use substitution to solve the system of equations.
{(4x+2y=-8),(y=-2x-4):}
The equation -8 = -8 is an identity. Thus, there are an infinite number of solutions.
When graphed, the equations are the same line.
400
Use elimination to solve the system of equations.
{(10x+5y=30),(5x-3y=-7):}
(1,4)
400
Juliana wants to buy turquoise stones on her trip to Mexico to give to at least 4 of her friends. The gift shop sells small stones for $4 or big stones for $6 each. Juliana has no more than $30 to spend.
Write a system of inequalities to represent this situation where
x = # of small stones and
y= # of big stones
List three viable solutions.
(2,3), (1,4), (0,4), (0,5), (1,3), (2,2), (3,1), (4,0)
(5,0), (6,0), (7,0), (3,2), (3,3), (6,1), (5,1), (4,1), (4,2),
400
Determine if the following equations are parallel, perpendicular, or neither.
y=1/4x+3
4x+y=3
perpendicular.
500
Create a system of equations that would have no solution.
Any equation that has the same slope, different y intercept.
500
Brandon has two equal sized large pitchers and two equal sized small pitchers. All of the pitchers together hold 40 cups of water. The capacity of one large pitcher minus the capacity of one small pitcher is 12 cups. How many cups can each type of pitcher hold?
Let
x = large pitcher
y = small pitcher
{(2x+2y=40),(x-y=12):}
x = 16 ; y =4
500
Jonathan's comic book collection consist of single issues that cost $4 each and paperback collections that cost $12 each. He has 100 books in all. His collection cost him $616. Write and solve a system of equations to determine how many single ussues and paperbacks Jonathan has in his collection.
Let c = number of single issue comics;
p = the number of paperback collections.
{(c+p=100),(4c+12p=616):}
Jorge has 73 single issue comics and 27 paperback collections.
500
One inequality in a system is 3x – y > 4. Write a second inequality so that the system will have no solution.
There is more than one correct answer.
Sample answer: y>3x+1
500
Estimate to the nearest tenth
sqrt22
4.7