Linear Functions
Systems of Linear Equations
Word Problems
100
Find the slope and y-intercept of
y=-3/5x + 4
slope: -3/5
y-intercept: 4
100
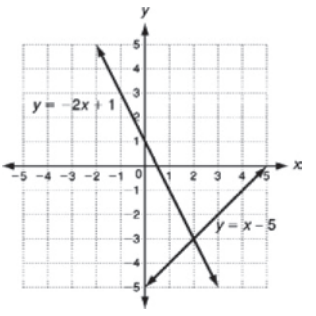
How can you represent the solution to system of equations graphed below?
An ordered pair or point.
100
Anthony is buying carrots and celery at the grocery store. The carrots cost $1.50 per pound and the celery costs $1.25 per pound. He has $10 to spend.
Write an equation in standard form to represent how he can split up his purchases.
1.5x+1.25y=10
200
Find the x-intercept and y-intercept of
3x+5y=30
x-intercept: 10
y-intercept: 6
200
How many solutions does the following system have?
{(y,=,1/3x,+,4),(y,=,1/3x,-,2):}
None. These are parallel lines.
200
T-Mobile charges $100 a month for a family plan for four people, but that doesn't include the cost of the phone. Tiana buys a phone for $600 and splits the cost of the phone plan with her family. Write a function to show how much money she spends on her phone and plan after m months.
f(m)=25m+600
300
Name two points on the graph of the linear function
2x-3y=6
(0,-2)
(3,0)
300
What is the first step you might take to solve the following system of equations?
{(2x,+,3y,=,11),(x,-,3y,=,-8):}
Add both equations
300
Mariko has 30 nickels and dimes. She has 12 more nickels than dimes. How many dimes does Mariko have?
{(x,+,y,=,30),(x,=,y,+,12):}
She has 9 dimes. (And 21 nickels!)
400
Name two points on the graph of the linear function
y=2x-10
(0,-10)
(1, -8)
400
What is the first step you might take to solve the following system of equations?
{(3x,+,y,=,13),(x,+,2y,=,11):}
Multiply the first equation by 2 or the second equation by 3.
400
Two pairs of socks and a pair of slippers cost $30. Five pairs of socks and a pair of slippers cost $42. How much does a pair of socks cost?
{(2x,+,y,=,30),(5x,+,y,=,42):}
A pair of socks costs $4.00. How much does a pair of slippers cost?
500
What is the y-intercept of a line with a slope of -2 that goes through the point (2,5)?
y-intercept: 9
500
Solve the following system of equations
{(3x,-,y,=,2),(-8x,+,2y,=,4):}
(-4, -14)
500
A truckload of 10-pound and 50-pound bags of fertilizer weighs 9000 pounds. A second truck carries twice as many 10-pound bags and half as many 50-pound bags as the first truck. That load also weighs 9000 pounds. How many of each bag are on the first truck?
x: number of 10-pound bags
y: number of 50-pound bags
{(10x,+,50y,=,9000),(20x,+,25y,=,9000):}
There are 300 10-pound bags and 120 50-pound bags on the first truck.