Graphing Systems of Linear Equations
Substitution Method
Elimination Method
Writing Systems of Linear Equations
100
Name the different types of solution
One solution, no solution, & infinitely many solutions
100
What is the first step when using the substitution method?
Isolate one of the variables by using inverse operations.
100
What is the first step when using elimination method?
Align each equation so that like variables are organized into columns.
100
Define the variables.
Savannah went into a movie theater and bought 9 bags of popcorn and 8 candies, costing a total of $87.50. Katherine went into the same movie theater and bought 3 bags of popcorn and 2 candies, costing a total of $26. Write a system of equations that could be used to determine the price of each bag of popcorn and the price of each candy. Define the variables that you use to write the system.
b = price of each bag of popcorn
c = price of each candy
200
What type of solution is represented on this graph?
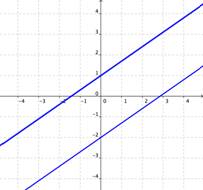
No solution
200
Use substitution method to solve this system.
y = -6x
y = -5x + 3
(-3, 18)
200
Use elimination method to solve this system.
-3x - 8y = -25
6x + 8y = 10
(-5,5)
200
Write the system of linear equations that represents this real world problem.
The drama club is selling tickets to their play to raise money for the show's expenses. Each student ticket sells for $7.50 and each adult ticket sells for $12.50. There was a total of $822.50 in revenue from the sale of 79 total tickets. Write a system of equations that could be used to determine the number of student tickets sold and the number of adult tickets sold.
7.50s + 12.50a = 822.50
s + a = 79
300
Graph this system of linear equations to find the solution.
y = -x + 2
y = 2x - 4
(2,0)
300
Use substitution method to solve this system.
4x - 7y = -2
x = 2y
(4, -2)
300
Use elimination method to solve this system.
5x + 4y = 40
6x + 4y = 44
(4,5)
300
Write the system of linear equations that represents this real world problem.
Emma runs a farm stand that sells apples and blueberries. Each pound of apples sells for $3 and each pound of blueberries sells for $1.25. Emma made $58.50 from selling a total of 30 pounds of apples and blueberries. Write a system of equations that could be used to determine the number of pounds of apples sold and the number of pounds of blueberries sold.
3a + 1.25b = 58.50
a + b = 30
400
Graph this system of equations to find the solution.
y = -2x - 2
2x - 3y = -18
(-3,4)
400
Use substitution method to solve this system.
-2x - 7y = -23
-5y + 7 = x
(22, -3)
400
Use elimination method to solve this system.
4x - 8y = 16
8x - 9y = 39
(6,1)
400
Write and solve this system of equations represented in this real world problem.
Amelia and her friend Joseph are going to a carnival that has games and rides. Amelia played 7 games and went on 10 rides and spent a total of $32. Joseph played 2 games and went on 5 rides and spent a total of $14.50. Determine the cost of each game and the cost of each ride.
Each game costs $1 and each ride costs $2.50.
500
Graph this system of linear equations to find the solution.
2x + y = -6
x - y = 3
(-1,-4)
500
Use substitution method to solve this system.
6x + 9y = 48
3x + y = 3
(-1,6)
500
Use elimination method to solve this system.
3x - 3y = 0
15x + 6y = 42
(2,2)
500
Write and solve the system of equations.
Jonathan and his children went into a bakery and he bought $5 worth of donuts and cookies. Each donut costs $1 and each cookie costs $0.50. He bought a total of 8 donuts and cookies altogether. Write and solve the system of equations to determine the number of cookies and the number of donuts Jonathan bought.
Jonathan bought 2 donuts and 6 cookies.